Obtain a relation log10.k2k1=Ea(T2−T1)2.303R×T1×T2
obtain a relation showing variation in rate constant with temeprature .
By Arrhenius equaiton , the rate constant k of the reaction at a temperature T is repesented as .
k=A×e−Ea/RT where A is a frequncy factore, R is a gas constant and Ea is the energy of activation.
By taking logarithm to the base we, get
In = In (A×−Ea/RT)
= In A+lne−Ea/RT=InA−EaRT In e
∴Ink=InA−EaRT
∴2.303log10k=2.303log.A10−EaRT
∴log10K=log10A−Ea2.303RT
If k1 and k2 are the rate constsnts at temperatures T1 and T2 respectively, then
log10k1=log10A−Ea2303RT1
log10k2=log10A−E2.303RT2
∴log10k2−log10k1=[log10A−Ea2.303RT2]−[log10A−Ea2.303RT1]
log10.k2k1=Ea2.303RT−Ea2.303RT
=Ea2.303R(1T1−1T2) log10.k2k1=Ea(T2−T1)2.303RT1×T2
By measuring the rate constant k1 and k2 at two different temperatures T1 and T2 the energy of activation Ea of the reaction can be obtained .
Similar Questions
Variation of equilibrium constan K with temperature is given by van't Hoff equation
InK=ΔrS∘R−ΔrH∘RT
for this equation, (ΔrH∘) can be evaluated if equilibrium constans K1 and K2 at two temperature T1 and T2 are known.
log(K2K1)=ΔrH∘2.303R[1T1−1T2]
Variation of log10 K with 1T is shown by the following graph in which straight line is at 45∘ hence ΔH∘ is :
View SolutionVariation of equilibrium constan K with temperature is given by van't Hoff equation
InK=ΔrS∘R−ΔrH∘RT
for this equation, (ΔrH∘) can be evaluated if equilibrium constants K1 and K2 at two temperature T1 and T2 are known.
log(K2K1)=ΔrH∘2.303R[1T1−1T2]
For an isomerization X(g)⇔Y(g) the temperature dependency of equilibrium constant is given by :
lnK=2−1000T
The value of ΔrS∘ at 300K is :
View Solution
Knowledge Check
When the temperature is increased, heat is supplied which increases the kinetic energy of the reacting molecules. This shall increase the number of collisions and ultimately the rate of reaction shall be enhanced. Arrhenius suggested a equation which describes K as a function of temperature, i.e.
k=Ae−Ea/RT
where
k= rate constant
A= a constant (frequency factor)
Ea= energy of activation
log10k=log10A−Ea2.303R[1R]
Y=C+MX
It is the equation of straight line with negative slope. On plotting log10k against [1T] we get a straight line as shown below :
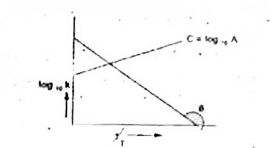
The slope gives activation energy and intercept gives frequency factor.
Also log.k2k1=Ea2.303[T2−T1T1T2]
The rate of certain reaction increases by 2.5 times when the temperature is raised from 300K to 310K. If k is the rate constant at 300K then rate constant at 310K will be equal toAkB2kC2.5kD13kThe efffect of temperature on equilibrium consatant is expressed as,
log[K2K1]=−ΔH2.303[1T2−1T1],(T2>T1)
For endothermic reaction false statement is :
(d) K2K1.A(T2>T1) =positiveBΔH=positiveClogK2>logK1DK2K1.
Variation of equilibrium constan K with temperature is given by van't Hoff equation
InK=ΔrS∘R−ΔrH∘RT
for this equation, (ΔrH∘) can be evaluated if equilibrium constans K1 and K2 at two temperature T1 and T2 are known.
log(K2K1)=ΔrH∘2.303R[1T1−1T2]
For an isomerization X(g)⇔Y(g) the temperature dependency of equilibrium cohnstant is given by :
lnK=2−1000T
The value of ΔrS∘ at 300K is :
View SolutionThe rate constant 'k'. For a reaction varies with temperature 'T' according to the question. logk=logA−Ea2.303R(1T)
Where Ea is the activation energy. When a graph is plotted for logkvs1/T, a straight line with a slope of −4250 K is obtained. Calcualte Ea for this reaction.
View SolutionHow is half-life period (t1/2) of a first order reaction related to its rate constant (k) ?
View SolutionRate constant 'k' of a reaction varies with temperature 'T' according to the equation:
logK=logA−Ea=Ea2.303R(1T)
where Ea is the activation energy. When a graph is plotted for log ,kvs1T a straight line with a slope of - 4250 K is obtained. Calculate ‘Ea' for the reaction. (R= 8.314 JK−1mol−1)
View SolutionRate constant k of a reaction varies with temperature according to equation:
logk= constant −Ea2.303R.1T
What is the activation energy for the reaction. When a graph is plotted for log k versus 1T a straight line with a slope-6670 K is obtained. Calculate energy of activation for this reaction (R=8.314 JK−1mol− 1)
View SolutionRate constant k of a reaction varies with temperature according to the equation
logk = constant −Ea2.303R(1T)
where Ea is the energy of activation for the reaction . When a graph is plotted for log k versus 1T , a straight line with a slope - 6670 K is obtained. Calculate the energy of activation for this reaction
View Solution
