The number density of molecules of a gas depends on their distance r from the origin as, n(r)=n0e−αr4. Then the total number of molecules is proportional to :
n0α−3/4
√n0α½
n0αa/4
n0α−3
The correct Answer is:A
To solve the problem, we need to find the total number of molecules, N, given the number density n(r)=n0e−αr4. The total number of molecules can be calculated by integrating the number density over the entire volume.
1. Understanding the Volume Element:
The volume element in spherical coordinates is given by:
dv=4πr2dr
2. Setting Up the Integral:
The total number of molecules N can be expressed as:
N=∫∞0n(r)dv
Substituting for n(r) and dv:
N=∫∞0n0e−αr4(4πr2)dr
This simplifies to:
N=4πn0∫∞0r2e−αr4dr
3. Changing Variables:
To solve the integral ∫∞0r2e−αr4dr, we can use a substitution. Let:
u=αr4⇒du=4αr3dr⇒dr=du4αr3
From the substitution, we have r2=(uα)14 and r3=(uα)34.
4. Changing Limits:
When r=0, u=0 and when r→∞, u→∞.
5. Substituting in the Integral:
The integral becomes:
∫∞0r2e−αr4dr=∫∞0(uα)14e−udu4α(uα)34
Simplifying this gives:
=14α∫∞0u14α14e−udu=14α34∫∞0u14e−udu
6. Using the Gamma Function:
The integral ∫∞0u14e−udu is related to the Gamma function:
Γ(54)=∫∞0u14e−udu
7. Final Expression for N:
Thus, we have:
N=4πn0⋅14α34⋅Γ(54)
This shows that N is proportional to n0α−34.
Conclusion:
The total number of molecules N is proportional to:
N∝n0α−34
The volume element in spherical coordinates is given by:
dv=4πr2dr
The total number of molecules N can be expressed as:
N=∫∞0n(r)dv
Substituting for n(r) and dv:
N=∫∞0n0e−αr4(4πr2)dr
This simplifies to:
N=4πn0∫∞0r2e−αr4dr
To solve the integral ∫∞0r2e−αr4dr, we can use a substitution. Let:
u=αr4⇒du=4αr3dr⇒dr=du4αr3
From the substitution, we have r2=(uα)14 and r3=(uα)34.
When r=0, u=0 and when r→∞, u→∞.
The integral becomes:
∫∞0r2e−αr4dr=∫∞0(uα)14e−udu4α(uα)34
Simplifying this gives:
=14α∫∞0u14α14e−udu=14α34∫∞0u14e−udu
The integral ∫∞0u14e−udu is related to the Gamma function:
Γ(54)=∫∞0u14e−udu
Thus, we have:
N=4πn0⋅14α34⋅Γ(54)
This shows that N is proportional to n0α−34.
The total number of molecules N is proportional to:
N∝n0α−34
Topper's Solved these Questions
Similar Questions
The potential energy of gas molecules in a certain certral field depends on the distance r from the field's centre as u(r)=ar, where a is a positive constant. The gas temperature is T, the concentration of molecules at the centre of the field is n0 Find :
(a) the number of molecules located at the distances between r and r+dr from the centre of the field ,
(b) the most probable distance separating the molecules from the centre of the field ,
( c) the fraction of molecules located in the spherical layer between r and r+dr ,
(d) how many times the concentration of molecules in the centre of the field will change if the temperature decreases η times.
View SolutionLet f(n)=n∑r=0n∑k=r(kr). Find the total number of divisors of f(9).
View Solution
Knowledge Check
The mean free path of molecules of a gas (radius r) is inversely proportional to
Ar3Br2CrD√rThe mean free path of molecules of a gas (radius r) is inversely proportional to
Ar3Br2CrD√rThe number of molecules per unit volume (n) of a gas is given by
APkTBkTPCPkTDRTP
A sphere of radius R_(0 carries a volume charge density proportional to the distance (x) from the origin, rho=alpha x where alpha is a positive constant.The total charge in the sphere of radius R_(0) is
View SolutionA : Number of air molecules in a room in winter is more than the number of molecules in the same room in summer.
R : At a given pressure and volume, the number of molecules of a given mass of a gas is directly proportional to the absolute temperature.
View SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)

where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
If PPc=Pr, TTc=Tr, and VmVm,c=Vr where
View Solutionthe electric field inside a sphere which carries a charge density proportional to the distance from the origin p=α r (α is a constant) is :
View SolutionThe graph show a hypothetical graph of gas molecules. N is the total number of molecules. Find the value of a.
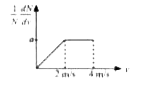
View Solution
