A set S is points in the xy-plane is symmetric about the origin, both coordinate axes If (2, 3) is in S, what is the smallest number of points in S?
Step by step video & image solution for A set S is points in the xy-plane is symmetric about the origin, both coordinate axes If (2, 3) is in S, what is the smallest number of points in S? by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
If a point lies in xy - plane then what is it z - coordinate?
View SolutionLet "S" be the set of all triangles in the xy-plane,each having one vertex at the origin and the other two vertices lie on coordinate axes with integral coordinates .If each triangle in "S" has area "60" sq.units,then the number of elements in the set "S" are
View Solution
Knowledge Check
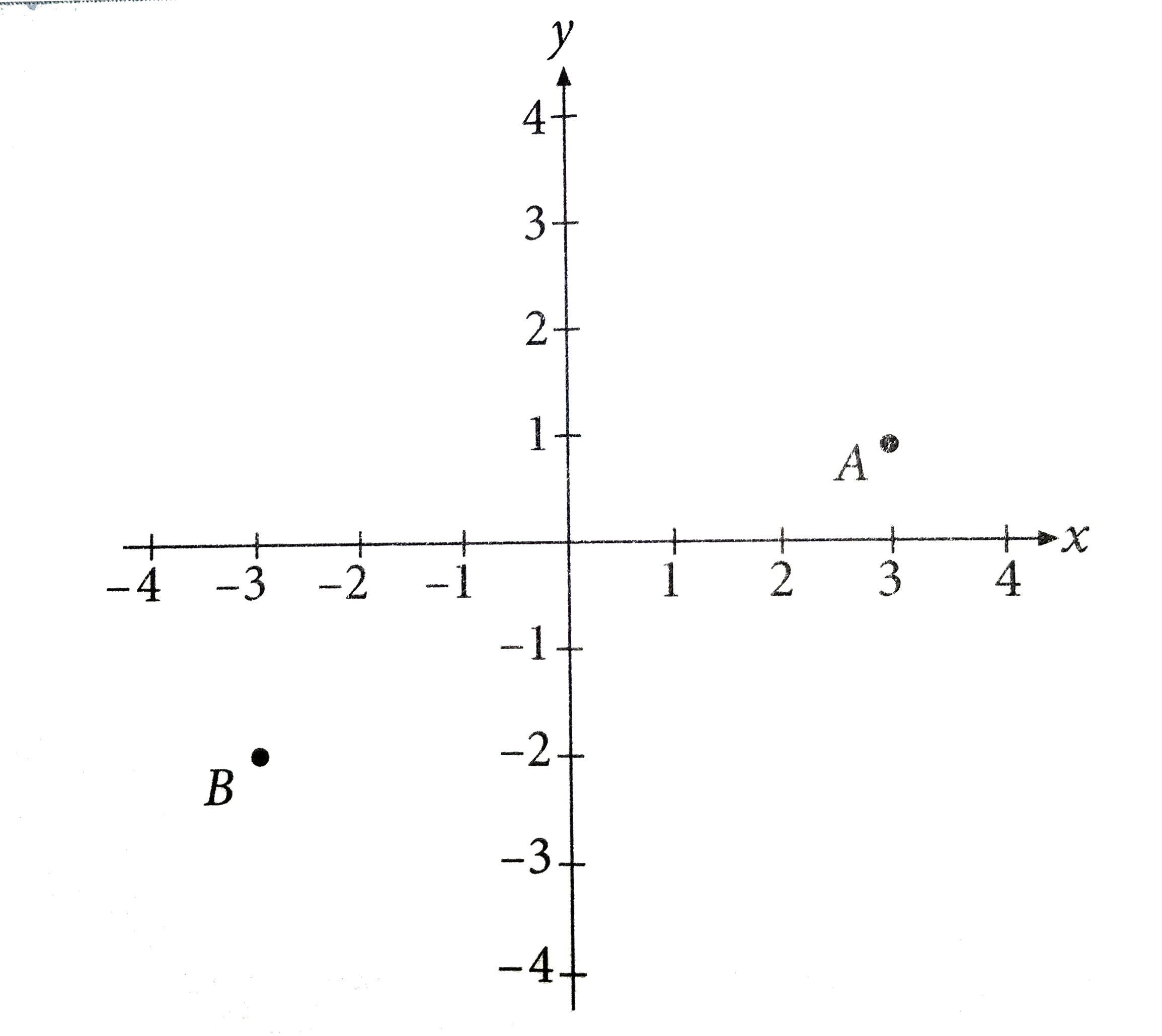
In the xy-plane above, what is the value of the x-coordinates of Point A minus the y-coordinates of Point B?A−2B−1C3D5Let S be the set of all triangles in the xy-plane, each having one vertex at the origin and the other two vertices lie on coordinate axes with integral coordinates. If each triangle in S has area 50 eq. units, then the number of elements in the set S is
A9B18C32D36Set S is the set of all points (x, y) in the coordinate plane such that x and y both integers with absolute value less than 4. If one of these points is chosen at random, what is the probability that this point will be 2 units or less from the origin ?
A0.189B0.227C0.265D0.314
Let S be the set of all triangles in the xy-plane, each having one vertex at the origin and the other two vertices lie on coordinate axes with integral coordinates. If each triangle in S has area 50 eq. units, then the number of elements in the set S is
View SolutionFind the components along the coordinate axes of the position vector of each of the following points: S(4,−3)
View SolutionFind the components along the coordinate axes of the position vector of each of the following points: S(4,−3)
View SolutionLet S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let P be a point on the circle S with both coordinates being positive. Let the tangent to S at P intersect the coordinate axes at the points M and N . Then, the mid-point of the line segment MN must lie on the curve (x+y)2=3xy (b) x2/3+y2/3=24/3 (c) x2+y2=2xy (d) x2+y2=x2y2
View SolutionLet S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let P be a point on the circle S with both coordinates being positive. Let the tangent to S at P intersect the coordinate axes at the points M and N . Then, the mid-point of the line segment MN must lie on the curve (x+y)2=3xy (b) x2/3+y2/3=24/3 (c) x2+y2=2xy (d) x2+y2=x2y2
View Solution
