A uniform field of 2.0NC−1 exists in space in x direction (a) Taking the potential at the origin to be zero, write an experssion for the potential at a general point (x,y,z). (b) At which points, the potential is 25V ? ( c) If the potential at the origin is taken to be 100V , what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero ? Is it parctical to choose the potential at infinity to be zero?
(a)E=2N/C∈x−direction
Potential at the origin is '0'
dV=−exdx−eydy−ezdz
⇒v−0=−2x⇒v=−2x
(b)(250−0)=−2x
⇒x=25−2=−12.5m
(c) If potential at the origin is 100V
V−100=−2x
⇒V=−2x+100=100−2x
(d)Potentialat≥≠ralp∮isv'−V=−2x
~v'=v+2x=0+2
Potential at origin is zero it is not practical to take potential at to be zero (Infinity)
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
8 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
Similar Questions
A uniform field of 8 N/C exists in space in positive x-direction.
(a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z).
(b) At which points, the potential is 160 V ?
(c) It the potential at the origin is taken to be 80V, what will be the expression for the potential at a general point ?
(d) What will be the potential at the origin if the potential at x = infinity is taken to be zero ?
View SolutionAn electric field →E=(25ˆi+30ˆj)NC−1 exists in a region of space.If the potential at the origin is taken to be zero then the potential at x=2 m y=2 m is :?
View Solution
Knowledge Check
Let V0 be the potential at the origin in an electric field →E=4ˆi+5ˆj. The potential at the point (x,y) is
AV0−4x−5yBV0+4x+5yC4x+5y−V0D−4x−5yLet V0 be the potential at the origin in an electric field →E=Exˆi+Eyˆj. The potential at the point (x,y) is
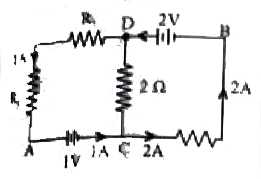
AV0−xEx−yEyBV0+xEx+yEyCxEx+yEy−V0D(√x2+y2)√E2x+E2y−V0In the given circuit the potential at point B is zero, the potential at points A and D will be
 AVA=4V,VD=9VBVA=3V,VD=4VCVA=9V,VD=3VDVA=4V,VD=3V
AVA=4V,VD=9VBVA=3V,VD=4VCVA=9V,VD=3VDVA=4V,VD=3V
An electric field →E=−−−−−−−→i20+→j30NC−1 exists in the space. If the potential at the origin is taken to be zero find the potential at (2m, 2m).
View SolutionAn electric field →E=Bxˆi exists in space, where B=20V/m2. Taking the potential at (2m, 4m) to be zero, find the potential at the origin.
View SolutionIn the circuit shown in the figure, if potentail at point A is taken to be zero, the potential at point B is
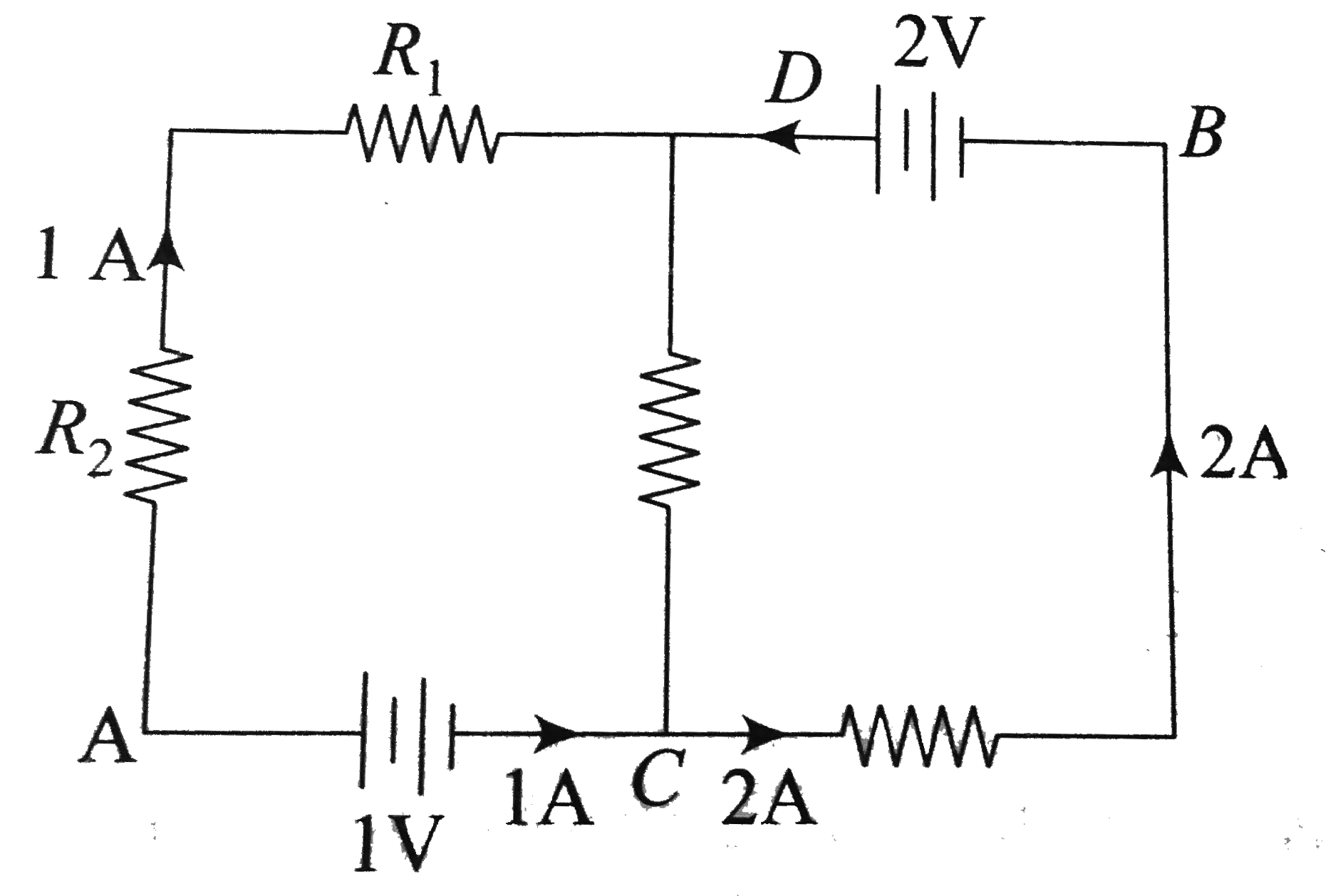
View SolutionIn the circuit shown in the figure, if the potential at point A behind to be zero, the potential at point B is :
View SolutionThe electric potential at a point (x,y,z) is given by V=−s2
View Solution
