The torque on a current loop is zero if the angle between the positive normal and the magnetic field is either θ=0 or θ=180∘. In which of the two orientations, the equilibrium is stable?
Step by step video & image solution for The torque on a current loop is zero if the angle between the positive normal and the magnetic field is either theta =0 or theta = 180^@. In which of the two orientations, the equilibrium is stable? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Objective 1
10 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Objective 2
10 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Worked Out Examples
11 Videos
- LIGHT WAVESBOOK - HC VERMACHAPTER - LIGHT WAVESEXERCISE - Exercises
41 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Exercises
61 Videos
Similar Questions
The torque on a current loop is zero if the angle between the positive normal and the magnetic field is either θ=0 or θ=180∘. In which of the two orientations, the equilibrium is stable?
View SolutionA rectangular loop of sides 10 cm and 5 cm carrying a current 1 of 12 A is placed in different orientations as shown in the figures below :
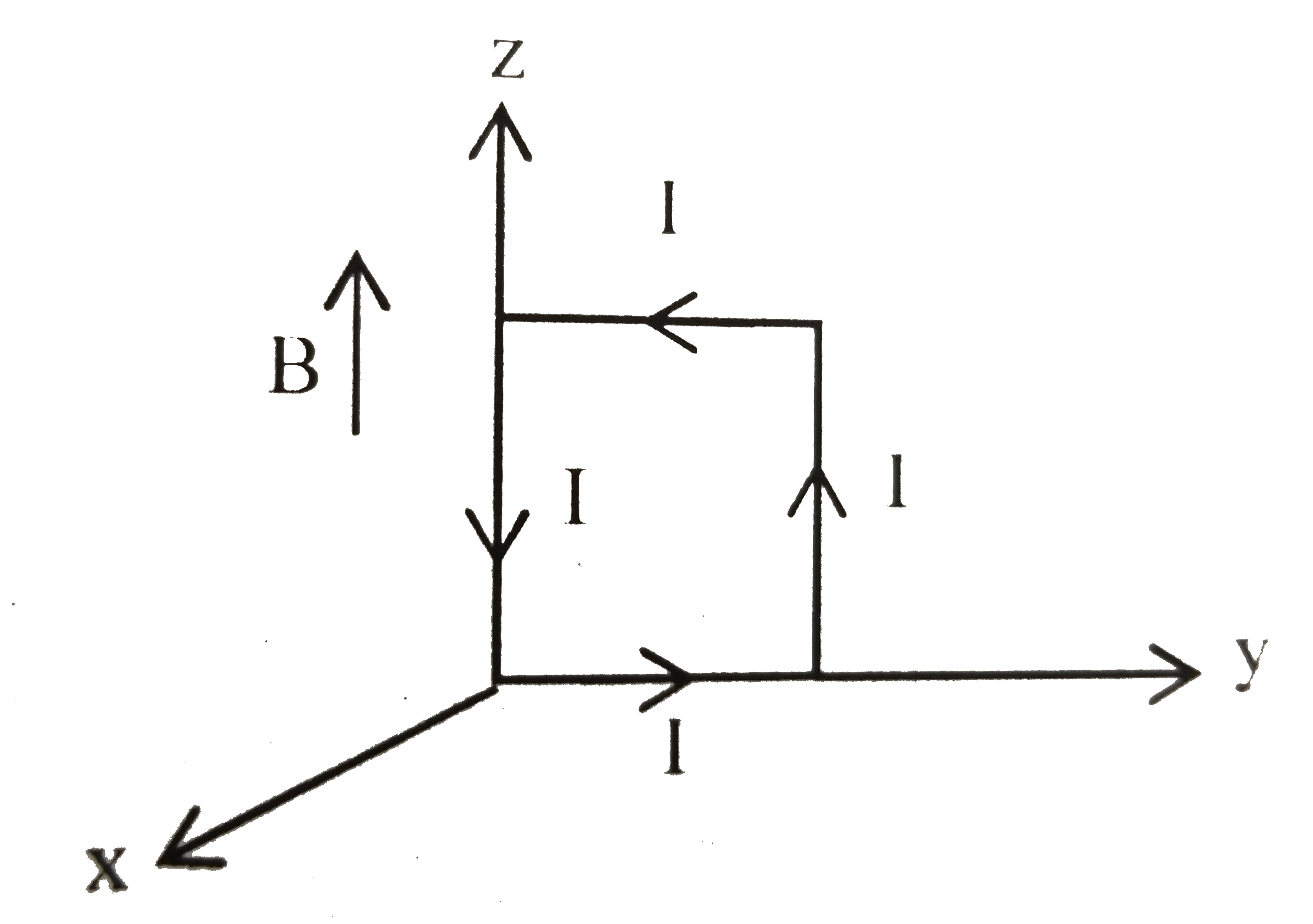
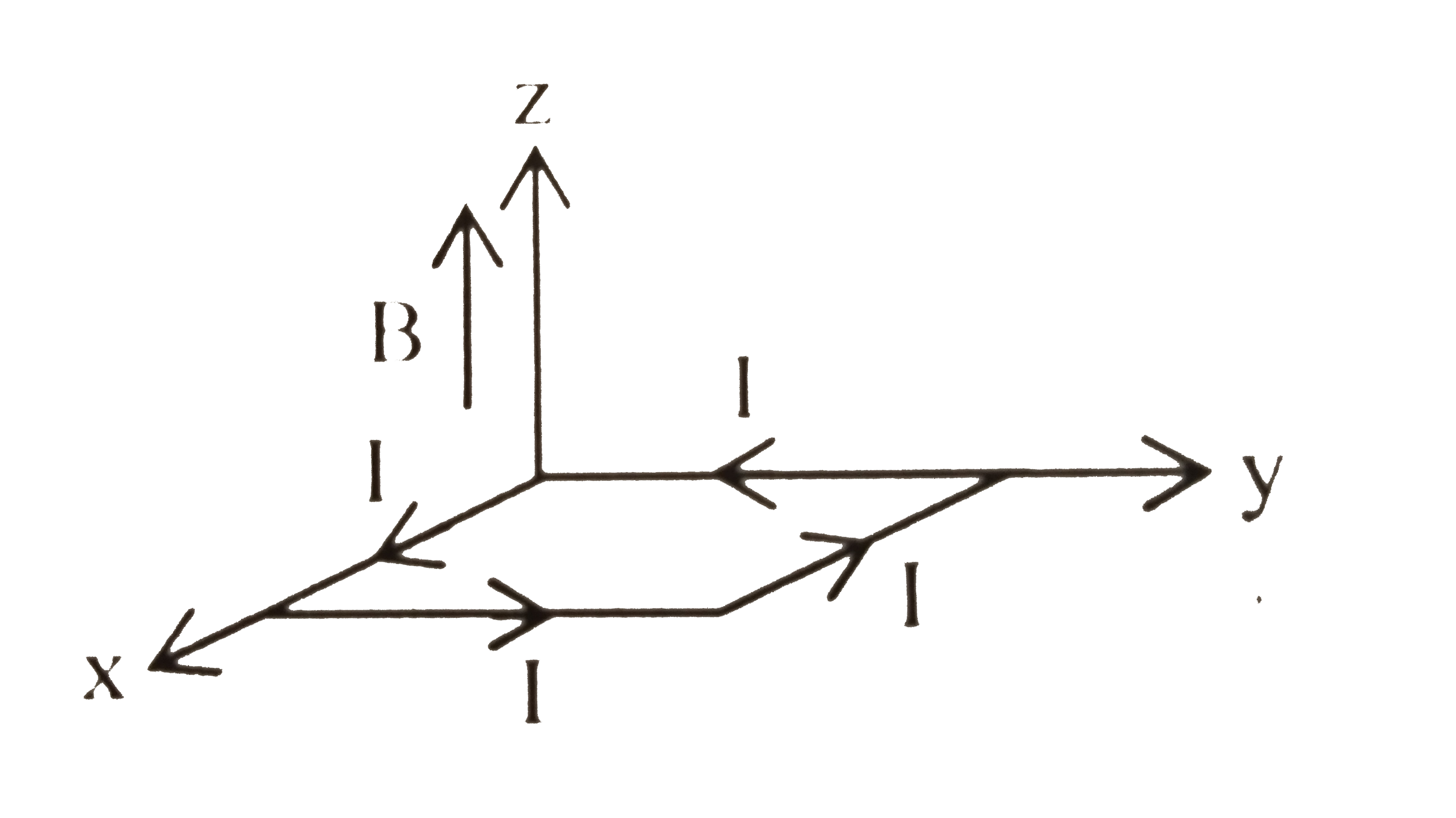
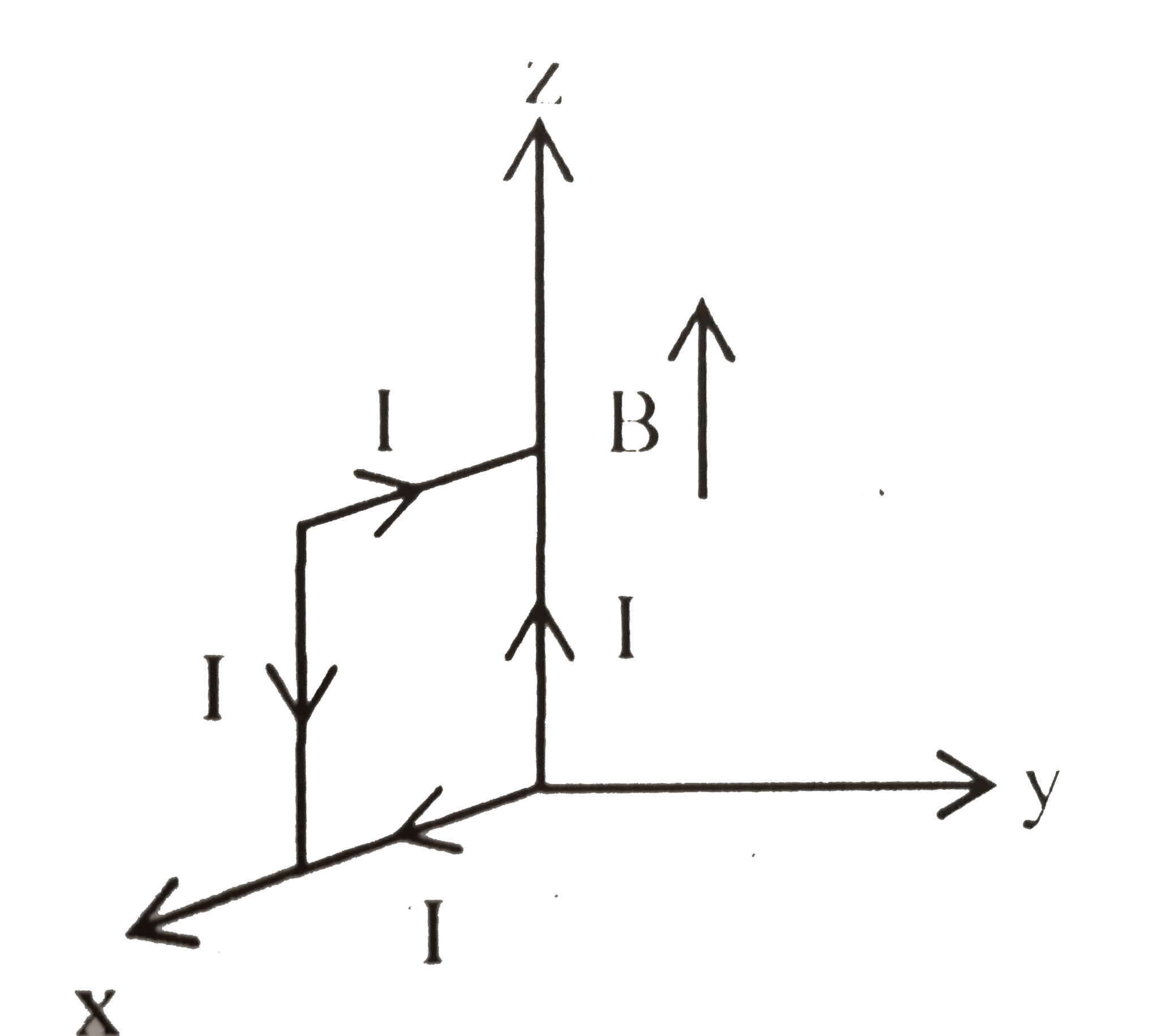
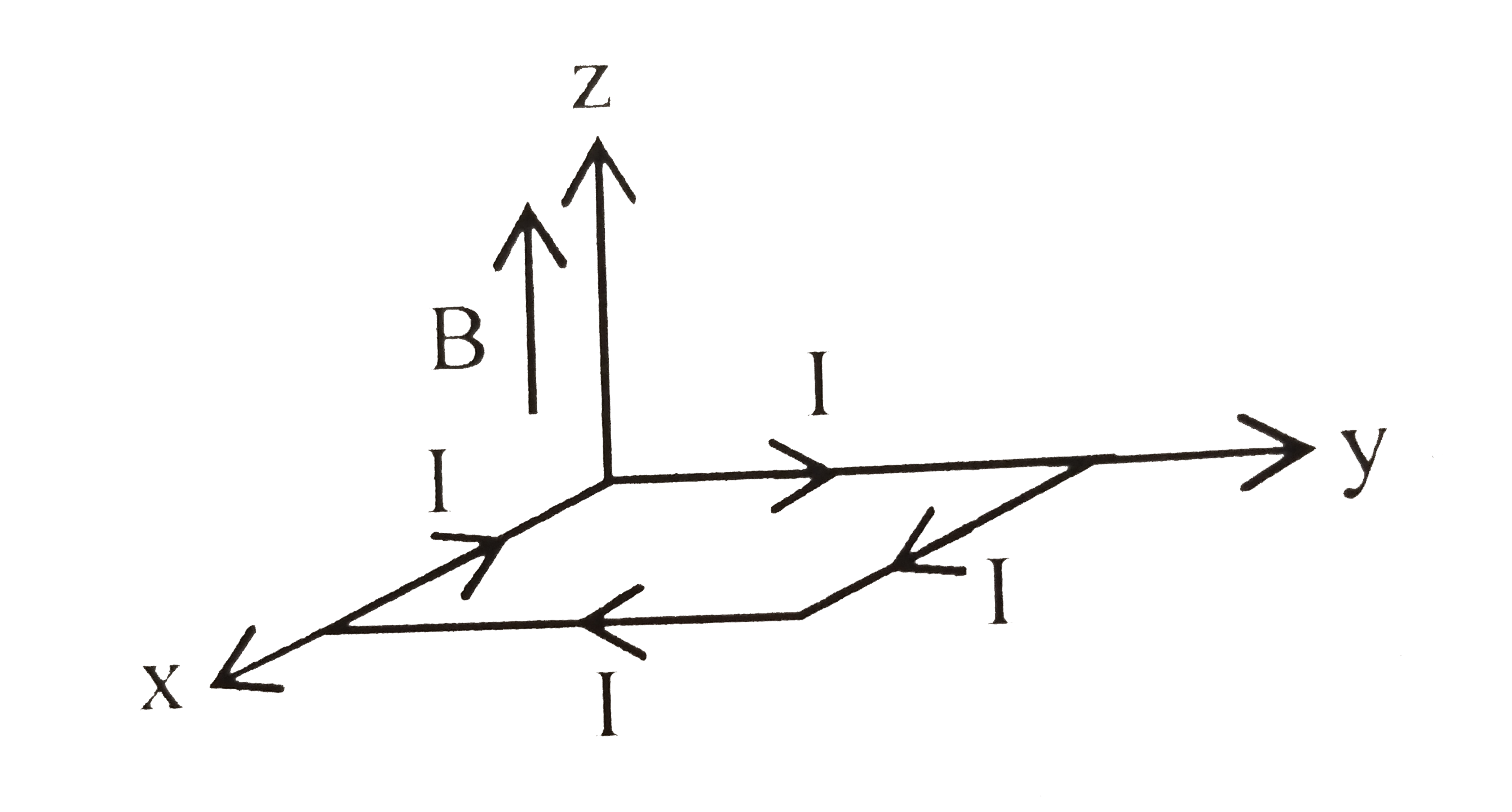 ltBrgt If there is a uniform magnetic field of 0.3 T in the positive z direction, in which orientations the loop would be in (i) stable equilibrium ?
ltBrgt If there is a uniform magnetic field of 0.3 T in the positive z direction, in which orientations the loop would be in (i) stable equilibrium ?
View Solution
Knowledge Check
Torque acting on a magnet held at angle θ with a magnetic field is maximum, where θ=
A0∘B90∘C360∘D90∘A rectangular loop of sides 10cmand5cm carrying a current 1of12A is placed in different orientations as shown in the figure below:
If there is auniform magnetic field of 0.3t in the positive z direction , in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?

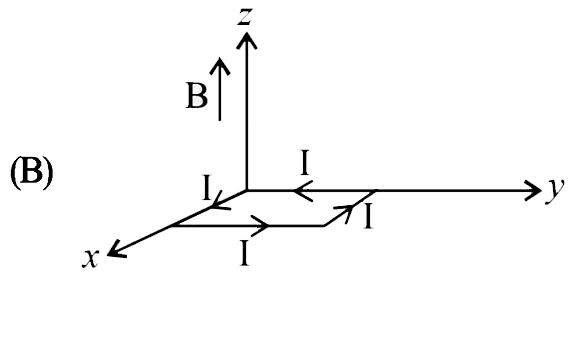

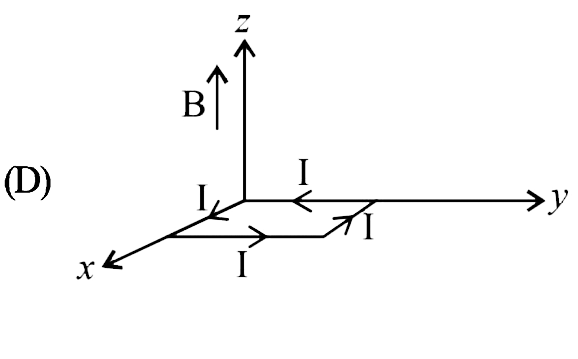 A(B)and(D) , respectivelyB(B)and(C) , respectivelyC(A)and(B) , respectivelyD(A)and(C) , respectively
A(B)and(D) , respectivelyB(B)and(C) , respectivelyC(A)and(B) , respectivelyD(A)and(C) , respectivelyA rectangular loop of sides 10 cm and 5 cm carrying a current I of 12 A is placed in different orientations as shown in the figures below ,
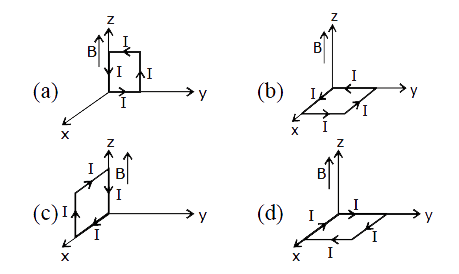
If there is a uniform magnetic field of 0.3 T in the positive z direction, in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?A(b) and (d), respectivelyB(b) and (c), respectivelyC(a) and (b), respectivelyD(a) and (c), respectively
Considering θ=π/2 as the zero-energy position of a current loop of magnetic moment m placed in a magnetic field of strength B,find the minimum potential energy. In what position is the potential energy minimum? Is this an equilibrium position ? What will be the work done in turning it through α from this position ? Examine whether you get the dame position for equilibrium and same value for work if θ=0 is taken as the zero-energy position.
View SolutionA bar magnet of magnetic moment 6 J/T is aligned at 60∘ with a uniform external magnetic field of 0.44 T. Calculate (a) the work done in turning the magnet to align its magnetic moment (i) normal to the magnetic field, (ii) opposite to the magnetic field, and (b) the torque on the magnet in the final orientation in case (ii).
View SolutionA bar magnet of magnetic moment 6 J/T is aligned at 60∘ with a uniform external magnetic field of 0.44 T. Calculate (a) the work done in turning the magnet to align its magnetic moment (i) normal to the magnetic field, (ii) opposite to the magnetic field, and (b) the torque on the magnet in the final orientation in case (ii).
View SolutionA rectangular loop of sides 10cm and 5cm carrying a current I of 12A is placed in different orienctations as shown in the figure
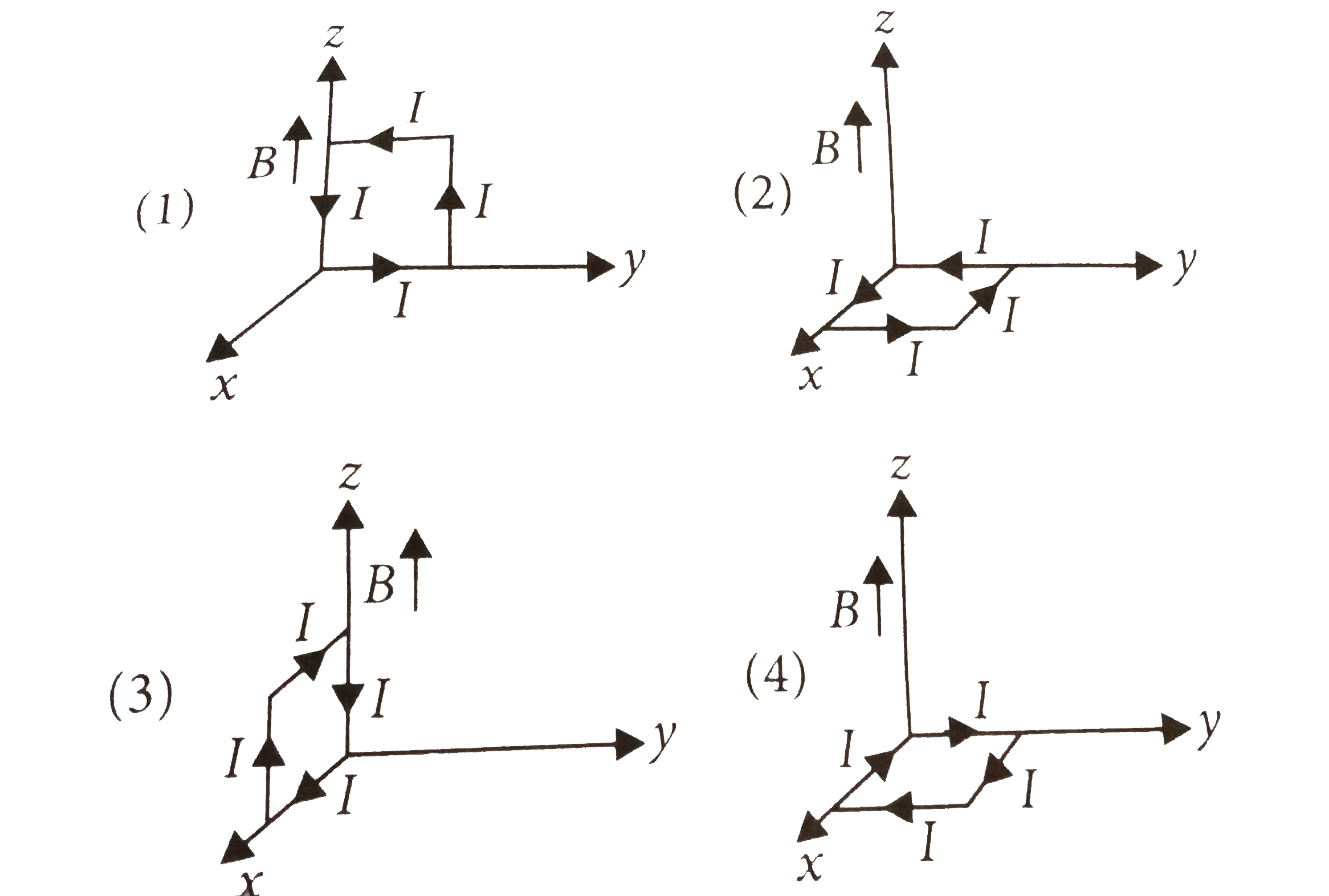
If there is a uniform magnetic field of 0.3 T in the positive z-direction, in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium .
View SolutionA circular coil of 100 turns and effective diameter 20cm carries a current of 0.5A. It is to be turned in a magnetic field of B=2.0T from a position in which the normal to the plane of the coil makes an angle θ equals to zero to one in which θ equals to 180∘. Thw work required in this process is
View Solution