A charged particle is whirled in a horizontal circle on a frictionless table by attaching it to a string fixed at one pint. If a magnetic field is switched on in the vertical direction, the tension in the string
will increase
will decrease
will remai the same
may increase or decrease
The correct Answer is:may increasec or decrease
To solve the problem of how the tension in the string changes when a magnetic field is applied to a charged particle being whirled in a horizontal circle, we can follow these steps:
1. Identify the Forces Acting on the Particle:
- The charged particle experiences two primary forces:
- The tension (T) in the string, which provides the centripetal force necessary for circular motion.
- The magnetic force (F_m) due to the magnetic field when it is turned on.
2. Centripetal Force Requirement:
- For an object moving in a circle of radius r with speed v, the required centripetal force is given by:
Fc=mv2r
- Initially, when the magnetic field is off, the tension in the string provides this centripetal force:
T=mv2r
3. Introduce the Magnetic Field:
- When the magnetic field B is turned on in the vertical direction, the charged particle experiences a magnetic force given by:
Fm=q(v×B)
- The direction of this force can be determined using the right-hand rule. Depending on the direction of the velocity v and the magnetic field B, the magnetic force can either act towards the center of the circle or away from it.
4. Analyze the Effect of the Magnetic Force:
- If the magnetic force Fm acts towards the center of the circle (in the same direction as the centripetal force), the tension in the string will decrease:
T′=mv2r−Fm
- If the magnetic force Fm acts away from the center (opposite to the centripetal force), the tension in the string will increase:
T′=mv2r+Fm
5. Conclusion:
- The tension in the string can either increase or decrease depending on the direction of the magnetic force relative to the centripetal force. Thus, the tension in the string may increase or decrease when the magnetic field is applied.
Final Answer:
The tension in the string may either increase or decrease depending on the direction of the magnetic force relative to the centripetal force.
- The charged particle experiences two primary forces:
- The tension (T) in the string, which provides the centripetal force necessary for circular motion.
- The magnetic force (F_m) due to the magnetic field when it is turned on.
- For an object moving in a circle of radius r with speed v, the required centripetal force is given by:
Fc=mv2r
- Initially, when the magnetic field is off, the tension in the string provides this centripetal force:
T=mv2r
- When the magnetic field B is turned on in the vertical direction, the charged particle experiences a magnetic force given by:
Fm=q(v×B)
- The direction of this force can be determined using the right-hand rule. Depending on the direction of the velocity v and the magnetic field B, the magnetic force can either act towards the center of the circle or away from it.
- If the magnetic force Fm acts towards the center of the circle (in the same direction as the centripetal force), the tension in the string will decrease:
T′=mv2r−Fm
- If the magnetic force Fm acts away from the center (opposite to the centripetal force), the tension in the string will increase:
T′=mv2r+Fm
- The tension in the string can either increase or decrease depending on the direction of the magnetic force relative to the centripetal force. Thus, the tension in the string may increase or decrease when the magnetic field is applied.
The tension in the string may either increase or decrease depending on the direction of the magnetic force relative to the centripetal force.
Topper's Solved these Questions
- MAGNETIC FIELDBook:HC VERMAChapter:MAGNETIC FIELDExercise:Objective 2
Explore 10 Videos
- MAGNETIC FIELDBook:HC VERMAChapter:MAGNETIC FIELDExercise:Exercises
Explore 61 Videos
- MAGNETIC FIELDBook:HC VERMAChapter:MAGNETIC FIELDExercise:Short Answer
Explore 10 Videos
- LIGHT WAVESBook:HC VERMAChapter:LIGHT WAVESExercise:Exercises
Explore 41 Videos
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMAChapter:MAGNETIC FIELD DUE TO CURRENTExercise:Exercises
Explore 61 Videos
Similar Questions
A stone with a mass of 0.9 kg is attached to one end of a string 0.8 m long. The string will break if its tension exceeds 500 N. The stone is whirled in a horizontal circle on a frictionless table top. The other end of the string is kept fixed. Find the maximum speed of the stone, it can attain without breaking the string.
View SolutionA particle of mass 21 g attached to a string of 70 cm length is whirled round in a horizontal circle. If the period of revolution is 2s, find the tension in the string.
View Solution
Knowledge Check
A stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
Am(gcosθ+ω2r)Bm√ω4r2+g2Cm√ω2r2+g2Dm(gcosθ−ω2r)A particle of mass m and charge Q is attached to a string of length l. It is whirled in a vertical circle in the region of an electric field E as shown in the figure-5.105.What is the speed given to the particle at the point B,so that tension in the string when the particle is at A is ten times the weight of the particle?
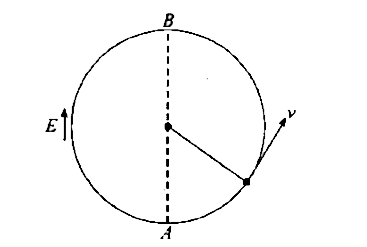 A√5glB√5(g−QEm)lC√QElmD√5(g+QEm)l
A√5glB√5(g−QEm)lC√QElmD√5(g+QEm)lA particle tied with a string is whirled along a vertcial circle.
AAcceleration of particle is always directed towards centreBAcceleration is directed along vertically downard when particle is at lowest positionCAcceleration at highest point cannot be less than g.DAcceleration is greater then 'g' where string is horizontal
calculate the tension in the string and angle made by it with vertical if electric field is directed in horizontal direction.
View SolutionA particle of mass 20 g is whirled into a vertical circle of radius 80cm using a massless string The speed of the particle when the string makes an angle 60∘ with the verticle line is 1.5ms−1 What is the tension in the string in this position ?
View SolutionA particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View SolutionA particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
View SolutionA mass 2 kg is whirled in a horizontal circle by means of a string at an initial speed of 5 revolutions per minute . Keeping the radius constant the tension in the string is doubled. The new speed is nearly
View Solution