A conducting loop of area 5.0cm2 is placed in a magnetic field which varies sinusodially with time as B=B0sinωt where B0=0.20T and ω=300s−1. The normal to the coil makes an angle of 60∘ with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ=(τ900)s and (c) the emf induced at t=(π600)s.
Here A=5cm2=5×10−4m2
B=B0sinωt=0.2sin(300t)
θ=60∘
(a)Maxe.m.f∈duced∈thecoil
e=(−dθ)(dt)=(dt)(BAcosθ)
=dt(B0sinωt×5×10−4×1/2)
=B0×52×10−4ddt(sinωt)
=B05210−4cosωt.ω
=0.2×52×300×10−4×cosωt
=15×10−3costωt.
emax=15×10−3=0.015V.
(b)Inducedemfatt=(π900)s
=e=15×10−3cosωt
=15×10−3×cos(300×π900)
=15×10−3×(12)
=0.01520=0.0075=7.5×10−3V
(c)Inducedemfatt=π600s
e=15×10−3×cos(300×π600)
=15×10−3×0=0V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
A conducting loop of area 5.0cm2 is placed in a magnetic field which varies sinusodially with time as B=B0sinωt where B0=0.20T and ω=300s−1. The normal to the coil makes an angle of 60∘ with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ=(τ900)s and (c) the emf induced at t=(π600)s.
View SolutionA conducting loop of area A is placed in a magnetic field which varies sinusoidally with time as B=B0sin
View Solution
Knowledge Check
A conducting looop of area 5.0cm2 is placed in a magnetic field which varies sinusoidally with time as B=0.2sin300t . The normal to the coil makes an angle of 60∘ with the field. The emf induced at t=(π/900)s
A7.5×10−3VBzeroC15×10−3VD20×10−3VA coil of 100 turns and area 5 square centimetre is placed in a magnetic field B = 0.2 T . The normal to the plane of the coil makes an angle of 60∘ with the direction of the magnetic field. The magnetic flux linked with the coil is
A5×10−3WbB5×10−5WbC10−2WbD10−4WbA coil having an area A0 is placed in a magnetic field which changes from B0 to 4B0 in time interval t. The emf induced in the coil will be
A3A0B0tB4A0B0tC3B0A0tDB0A0t
A conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
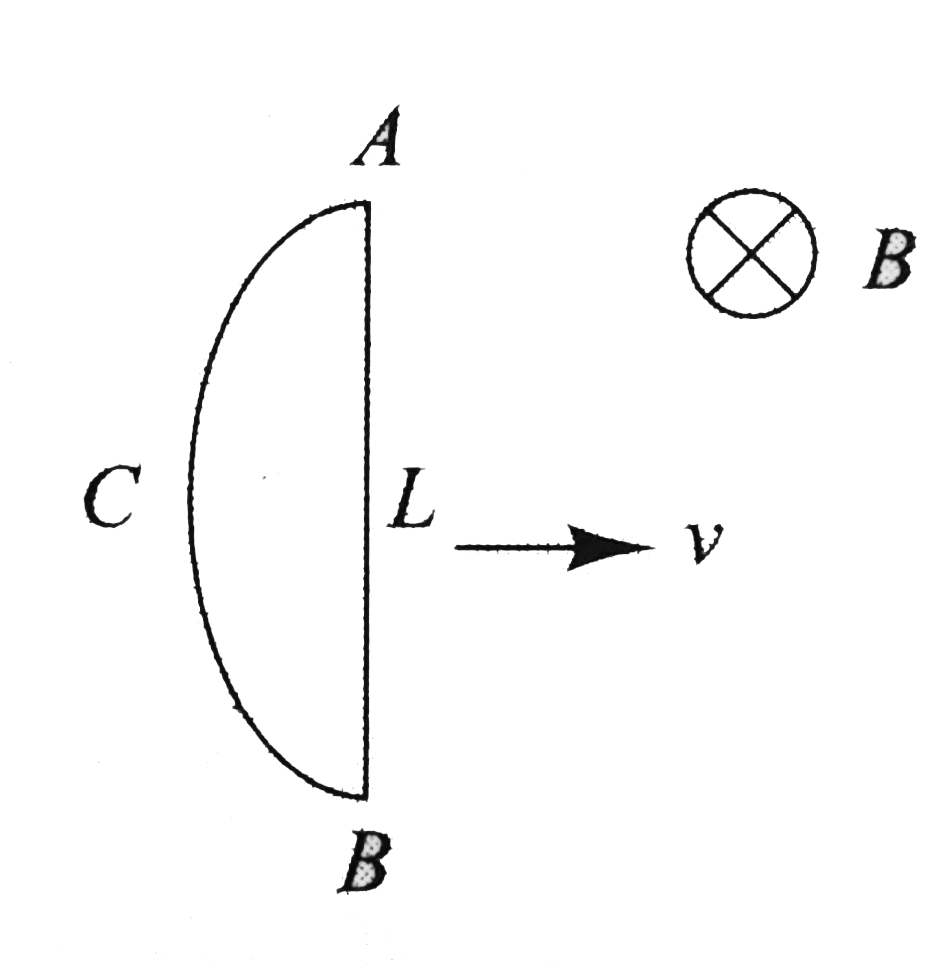
View SolutionShows a closed coil ABCL moving in a uniform magnetic field B with a velocity v.
Find
(a) emf induced in the coil.
(b) emf induced in curve part ACB and straight AB as vev(L)×→B
View SolutionA coil intercepts a magnetic flux of 0.2×10−2 Wb in 0.1 s. What is the emf induced in the coil ?
View SolutionA circular brass loop of radius a and resistance R is placed with it plane perpendicular to a magnetic field, which varies with time as B=B0sinωt. Obtain the expression for the induced current in the loop.
View SolutionA coil having an area A0 is placed in a magnetic field which changes from B0 to 4B0 in time interval t. The emf induced in the coil will be
View Solution
