The current in a long solenoid of radius R and having n turns per unit length is given by i=i0sinωt. A coil having N turns is wound around it near the centre. Find (a) the induced emf in the coil and (b) the mutual inductance between the solenoid and the coil.
To solve the problem, we need to find the induced emf in the coil and the mutual inductance between the solenoid and the coil. Let's break it down step by step.
Step 1: Determine the Magnetic Field Inside the Solenoid
The magnetic field B inside a long solenoid is given by the formula:
B=μ0ni
where:
- μ0 is the permeability of free space,
- n is the number of turns per unit length of the solenoid,
- i is the current flowing through the solenoid.
Given that the current i is i0sin(ωt), we can substitute this into the equation:
B=μ0n(i0sin(ωt))=μ0ni0sin(ωt)
Step 2: Calculate the Magnetic Flux Through the Coil
The magnetic flux Φ through one turn of the coil is given by:
Φ=B⋅A
where A is the area of the coil. The area A of the coil can be calculated as:
A=πR2
Thus, the total magnetic flux through N turns of the coil is:
Φtotal=NΦ=NBA=N(μ0ni0sin(ωt))(πR2)
So,
Φtotal=Nμ0ni0πR2sin(ωt)
Step 3: Find the Induced EMF in the Coil
According to Faraday’s law of electromagnetic induction, the induced emf E in the coil is given by the negative rate of change of magnetic flux:
E=−dΦtotaldt
Substituting the expression for Φtotal:
E=−ddt(Nμ0ni0πR2sin(ωt))
Calculating the derivative:
E=−Nμ0ni0πR2ωcos(ωt)
Thus, the induced emf in the coil is:
E=Nμ0ni0πR2ωcos(ωt)
Step 4: Calculate the Mutual Inductance
The mutual inductance M between the solenoid and the coil can be defined as:
M=Φtotali
Using the expression for Φtotal and substituting i=i0sin(ωt):
M=Nμ0nπR2i0sin(ωt)i0sin(ωt)=Nμ0nπR2
Final Answers
(a) The induced emf in the coil is:
E=Nμ0ni0πR2ωcos(ωt)
(b) The mutual inductance between the solenoid and the coil is:
M=Nμ0nπR2
The magnetic field B inside a long solenoid is given by the formula:
B=μ0ni
where:
- μ0 is the permeability of free space,
- n is the number of turns per unit length of the solenoid,
- i is the current flowing through the solenoid.
B=μ0n(i0sin(ωt))=μ0ni0sin(ωt)
The magnetic flux Φ through one turn of the coil is given by:
Φ=B⋅A
where A is the area of the coil. The area A of the coil can be calculated as:
A=πR2
Thus, the total magnetic flux through N turns of the coil is:
Φtotal=NΦ=NBA=N(μ0ni0sin(ωt))(πR2)
So,
Φtotal=Nμ0ni0πR2sin(ωt)
According to Faraday’s law of electromagnetic induction, the induced emf E in the coil is given by the negative rate of change of magnetic flux:
E=−dΦtotaldt
Substituting the expression for Φtotal:
E=−ddt(Nμ0ni0πR2sin(ωt))
Calculating the derivative:
E=−Nμ0ni0πR2ωcos(ωt)
Thus, the induced emf in the coil is:
E=Nμ0ni0πR2ωcos(ωt)
The mutual inductance M between the solenoid and the coil can be defined as:
M=Φtotali
Using the expression for Φtotal and substituting i=i0sin(ωt):
M=Nμ0nπR2i0sin(ωt)i0sin(ωt)=Nμ0nπR2
(a) The induced emf in the coil is:
E=Nμ0ni0πR2ωcos(ωt)
M=Nμ0nπR2
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
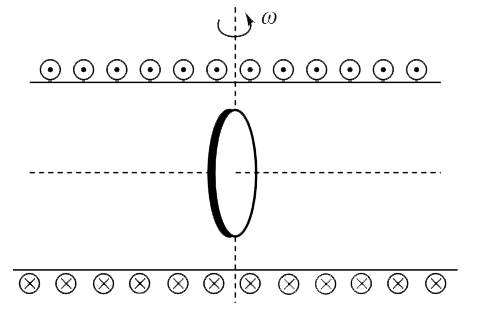
A long solenoid has n turns per unit length and carries a current i=i0sinωt. A coil of N turns and area A is mounted inside the solenoid and is free to rotate about its diameter that is perpendicular to the axis of the solenoid. The coil rotates with angular speed ω and at time t = 0 the axis of the coil coincides with the axis of the solenoid as shown in figure. Write emf induced in the coil as function of time.
View SolutionA conducting wire of 100 turns is wound over and near the centre of a solenoid of 100 cm length and 2 cm radius having 600 turns. Calculate mutual inductance of two coils.
View Solution
Knowledge Check
A conducting ring of radius b is placed coaxially in a long solenoid of radius a (b < a) having n turns per unit length. A current i=i0, cosωt flows through the solenoid. The induced emf in the ring is
AZeroBμ0ni0πa2ωCμ0ni0πa2cosωtDμ0ni0πb2ωcosωtThe magnetic field on the axis of a long solenoid having n turns per unit length and carrying a current is
Aμ0niBμ0n2iCμ0ni2Dnone of theseAn infinite long solenoid having n turns per unit length is shown in figure. The magnetic field at P, when a current I is flowing through it would be
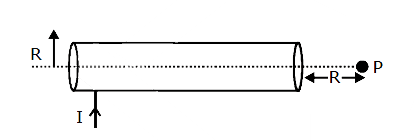 Aμ0nIBzeroCμ0nI2√2Dμ0nI2[1−1√2]
Aμ0nIBzeroCμ0nI2√2Dμ0nI2[1−1√2]
A long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
View SolutionThe magnetic field B within the solenoid having n turns per unit length and carrying a current I is given by
View SolutionThere is a long solenoid of radius 'R' having 'n' turns per unit length with current i flowing in it. A particle having charge 'q' and mass 'm' is projected with speed 'v' in the perpendicular direction of axis from a Point on its axis. Find maximum value of 'v' so that it will not collide with the solenoid.
View SolutionA solenoid of radius R number of turn per unit length n and length L has a current I=I0cosωt. The value of induced electric field at a distance of r outside the solenoid, is :
View SolutionA solenoid of radius 2.50cm has 400turns and a length of 20.0cm. The current in the coil is changing with time such that to produce an emf of 75.0 mV.
the self-induced emf in the solenoid is
View Solution