Figure shows a small, plane strip suspended from a fixed support through a string of length l. A continuous beam of monochromati clight is incident horizontally on the strip and is completely absorbed. The energy falling on the strip per unit time is W. (a) Find the deflection of the string from the vertical if the mirror stays in equilibrium. (b) If the strip is deflected slightly from its equilibrium position in the plane of the figure, what will be the time period of the resulting oscillations?

(a) The linear momentum of the light falling per unit time on the strip is W/c. As the light is incident on the strip, its momentum is absorbed by the mirror. The change in momentum imparted to the strip per unit time is thus W/c. This is equal to the force on the strip by the light beam, the weight of the strip and the force due to tension add to zero. If the string makes an angle theta with the vertical,
T cos theta = mg
andTsinθ=Wc.
Thus, tan(θ)=(Wmgc).
(b) In equilibrium, the tension is
T=⎛⎜⎝[(mg)2+(Wc)2]12⎞⎟⎠
or,Tm=⎛⎜⎝[(g2)+(Wmc)2]12⎞⎟⎠.
This plays the role of effective g. The time period of
small oscillations is
t=(2π(√lt/m))=2π⎛⎜
⎜
⎜
⎜
⎜⎝√l[(g2)+(Wmc)2]14.
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMACHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Short Answer
13 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMACHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Objective 1
14 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMACHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Worked Out Examples
2 Videos
- PERMANENT MAGNETSBOOK - HC VERMACHAPTER - PERMANENT MAGNETSEXERCISE - Exercises
25 Videos
- PHOTOMETRYBOOK - HC VERMACHAPTER - PHOTOMETRYEXERCISE - Exercises
16 Videos
Similar Questions
A thin plane strip is suspended from a fixed support through a string of length l. Material of the strip is such that is absorbs all the light falling on it. A parallel beam of light with power P moving horizontally is striking the plane strip . Find the angle made by string with the vertical if strip remains in equilibrium . If strip is slightly disturbed from its equilibrium position and then released , its equilibrium position and then released , what will be time period of resulting oscillation ?
View SolutionAlgorithm for area calculation using horizontal strips
View Solution
Knowledge Check
A particle of mass m is suspended from a fixed O by a string of length L. At t=0, it is displaced from its equilibrium position and released. The graph which shows the variation of the tension T in the string with time t is :
 A
A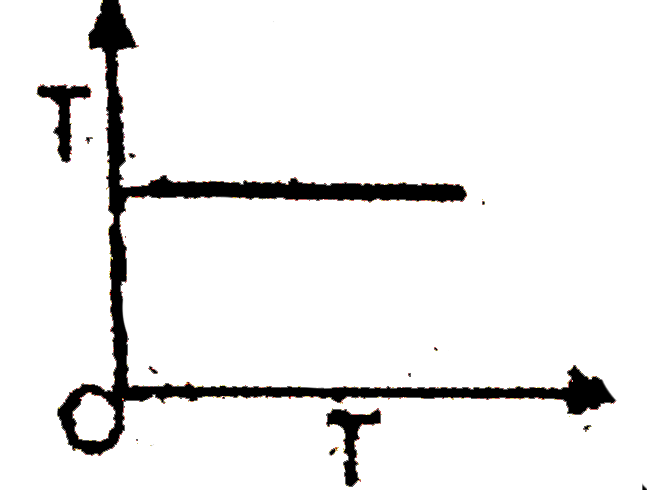 B
B C
C D
D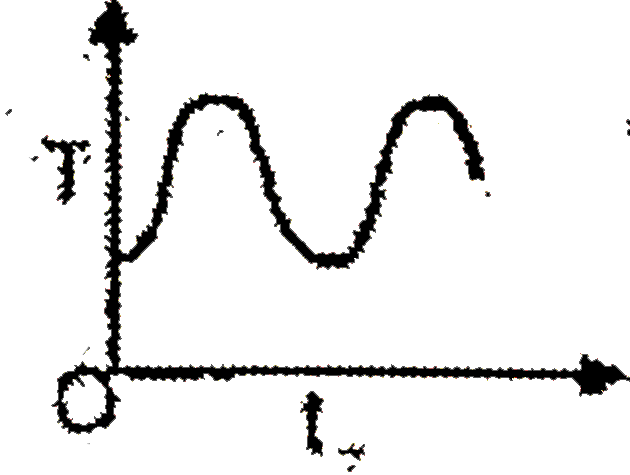
A small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
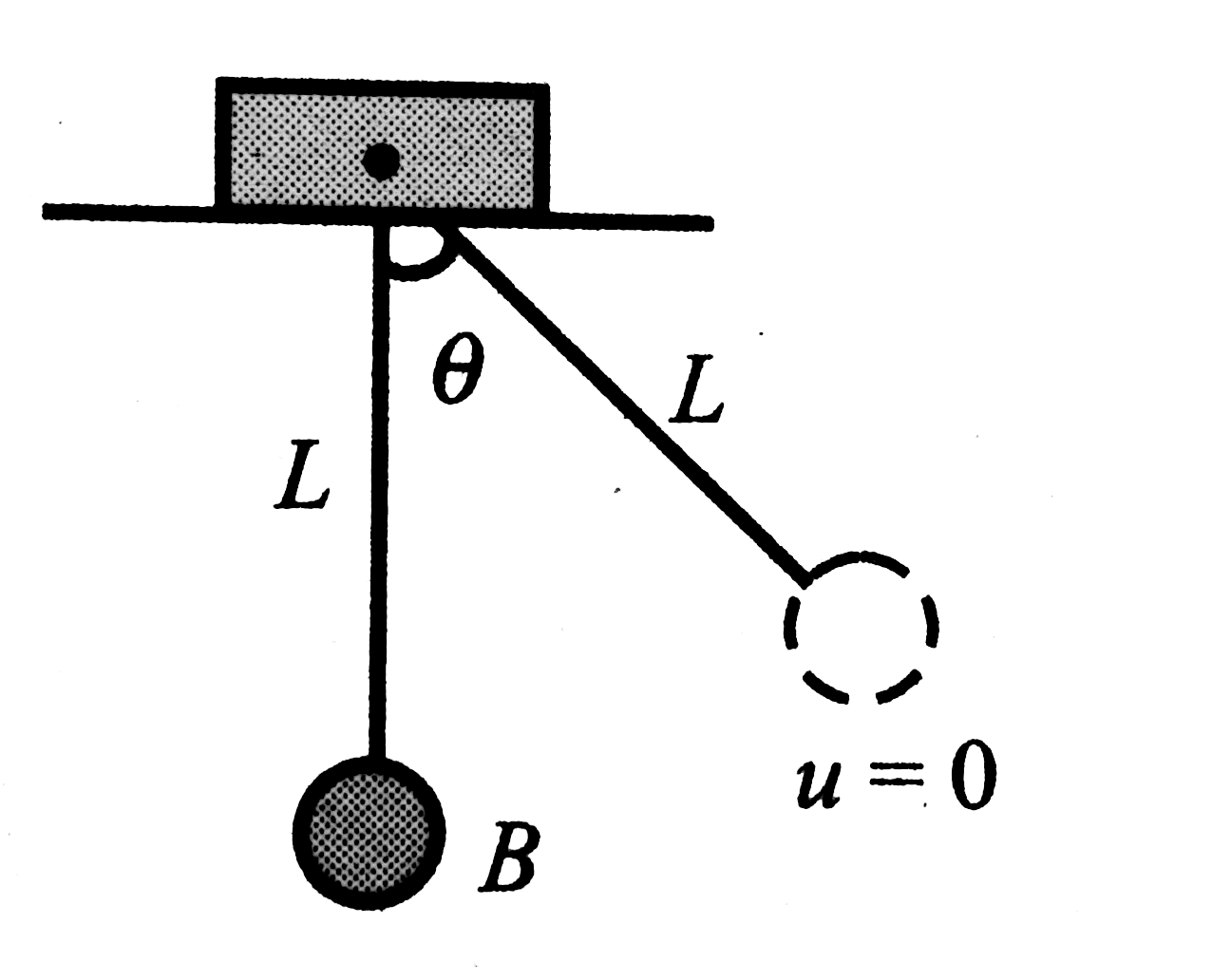
Tension in string when it is vertical, isAmgBmg(2−cosθ)Cmg(3−2cosθ)Dnone of these
A particle of mass m is suspended from a fixed point O by a string length l.At t=0, it is displaced from its equilibrium position and released.If T is the tension in the string with time t, then the correct graph is
View SolutionA small ball is suspended from a fixed point 'O' by means of a light and inextensible string of length 'l'. The ball is first taken aside such that string becomes horizontal and then released from rest. At the borrom it collides with a fixed obstacle. The co-efficient of restitution is 'e'. Find the maximum angular deflection of the string after nth collision.
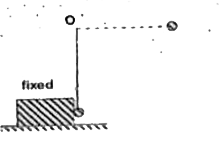
View SolutionA small ball is suspended from a fixed point 'O' by means of a light and inextensible string of length 'l'. The ball is first taken aside such that string becomes horizontal and then released from rest. At the borrom it collides with a fixed obstacle. The co-efficient of restitution is 'e'. Find the maximum angular deflection of the string after nth collision.

View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.

Tension in string when it is vertical, is
View SolutionArea calculation using horizontal strips for modulus function
View SolutionA particle is suspended by a light vertical inelastic string of length 1 from a fixed support. At its equilbrium position it is projected horizontally with a speed √6gl. Find the ratio of the tension in the string in its horizontal position to that in the string when the particle is vertically above the point of support.
View Solution
