A totally reflecting, small plane mirror placed horizontally faces a parallel beam of lighy as shown in figure. The mass of the mirror is 20g. Assume that there is no absorption in the lens and that 30% of the light emitted by the source goes through the lens. Find the power of the source needed to support the weight of the mirror. Take g= 10 m s^-2.
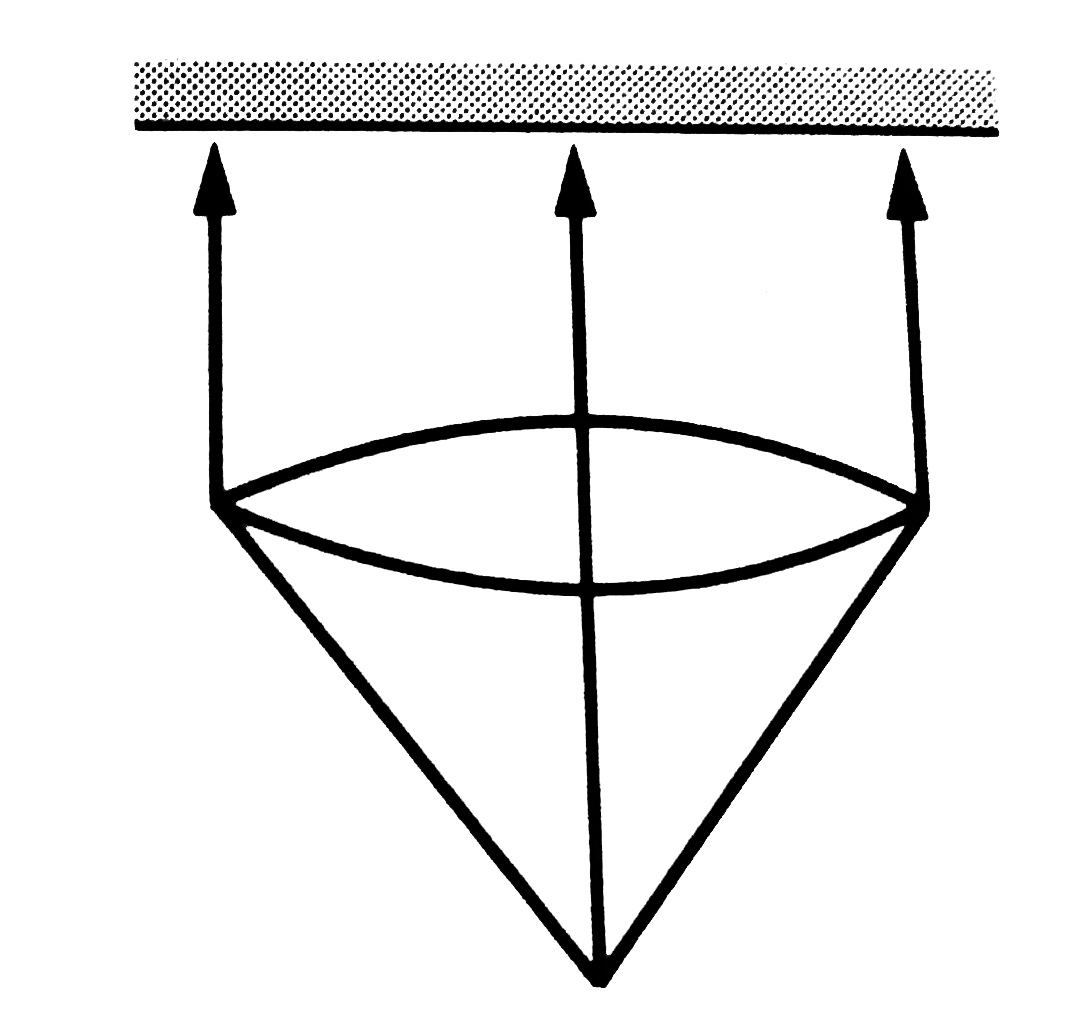
Here m=20g=20×10−3kg
The weight of the mirror is balanced. So, force exerted by the photons is equal to weight .
P=hλandE=hcλ=Pc
⇒Et=Ptc
⇒Rate of change of momentum
= power//c<br>30%oflightpassesthroughthe≤ns.<br>Thusitexertsforce,70%isref≤cted<br>:. Force exerted - 2
(rate of change of momentum)
=2×Power/c
30%(2×Powerθ)=mg
⇒Power=20×10−3×10×3×103×102×3
=10Wpower=100MW.
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMACHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Exercise
2 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMACHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Objective 2
7 Videos
- PERMANENT MAGNETSBOOK - HC VERMACHAPTER - PERMANENT MAGNETSEXERCISE - Exercises
25 Videos
- PHOTOMETRYBOOK - HC VERMACHAPTER - PHOTOMETRYEXERCISE - Exercises
16 Videos
Similar Questions
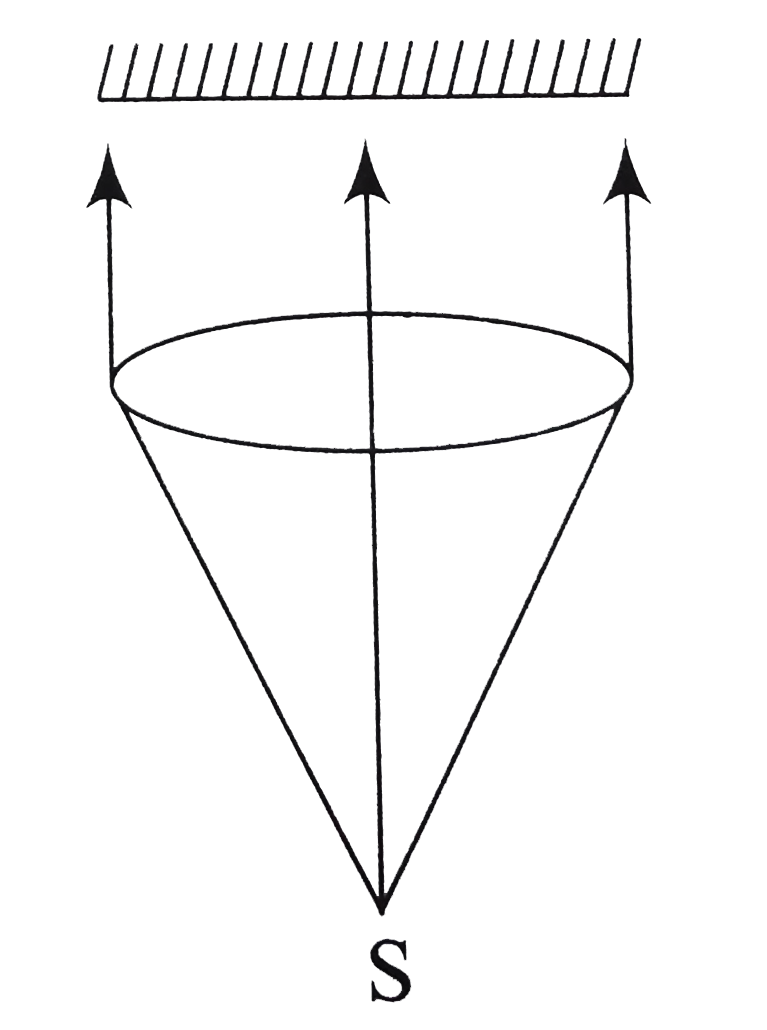
A totally reflecting, small plane mirror placed horizontally faces a parallel beam of light as shown in the Fig. The mass of the mirror is 20 g. Assume that there is no absorption in in the lens and that 30% of the light emitted by the source goes through the lens. Find the power (in×108W) of the source needed to support the weight of the mirror. Take g=10ms−2
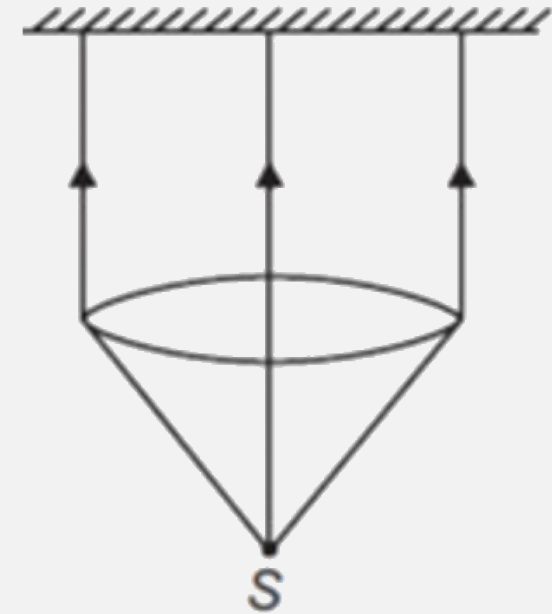
View SolutionA totally reflecting small plane mirror placed horizontally faces a parallel beam of light as shown in the figure. The mass of the mirror is 200 g. Assume that there is no absorption in the lens and that 20% of the light emitted by the source goes through the lens. The power of the source needs to support the weight of the mirror is P×108 watt, where P is [take g=10ms−2]
View Solution
Knowledge Check
A point source of light is placed at 2f from a converging lens of focal length f. A flat mirror is placed on the other side of the lens at a distanc d such that rays reflected from the mirror are parallel after passing through the lens again. If f = 30 cm, then d is equal to
A15 cmB30 cmC45 cmD75 cm
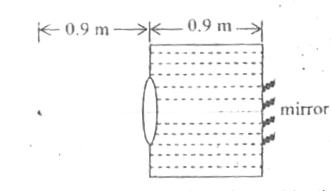
A thin equiconvex lens made of glass of refractive index 3/2 and of focal length 0.3m in air is sealed into an opening at one end of a tank filled with water (μ=32). On the opposite side of the lens, a mirror is placed inside the tank on the tank wall perpendicular to the lens axis as shown in Figure. The separation between the lens and mirror is 0.8m. A small object is placed outside the tank in front of the lens at a distance oa 0.9m from the lens along its axis. Find the position (relative to lens) of the image of the object formed by the system.

View SolutionA thin equiconvex lens of glass of refractive index μ=3/2 & of focal length 0.3min air is sealed into an opeing at one end of a tank filled with water (μ=4/3) .Ont he oppostie side of the lens ,a mirror is placed inside the tank on the tank wall perpendicualar tot he lens axis ,as shown in figure .the seperation bertween the lens and the mirror is 0.8mA small object is placed outside the tank in front of the lens at a distance of 0.9m form the lens along its axis .Find the position (relative to the lens)of the image of the object fromed byt he stsyem.

View SolutionA thin equiconvex lens of glass of refractive side of 3/2 and of focal length 0.3 m is sealed into an opening at end of a tank filled with water (p=4/3). on the opposite side of the lens a mirror is placed inside the tank with the tank wall perpendicular to the sense axis as shown in figure
The separation between the lens and mirror is 0.8 m. A small object is placed outside the tank is front of the lens, at a distance of 0.9 m from the lens along its axis. Find the position (relative to the lens) of the image of the object formed by the system.
View SolutionIn figure-2.40(a), we see a beam of length L pivoted at one end and supporting a 200 kg object at the other end. Find the tension T in the supporting cable that runs upward to the ceiling. Assume that the weight of the negligible. Take g=10m/s2
View SolutionA concave mirror of focal length 20cm and a convex lens of focal length 10(~cm) are kept with their optic axis parallel but separated by 0.5mm as shown in the figure.The distance between the lens and the mirror is 10cm. An object of height 3min is placed on the optical axis of the lens at a distance of 15∘cm from the lens. Find the height of the image (in mm ) formed by the mirror after retion from the lens.
'(##CEN_KSR_PHY_JEE_C26_E01_037_Q18##)'
View SolutionA converging lens and a diverging mirror are placed at a separation of 20 cm. The focal length of the lens is 30 cm and that of the mirror is 50 cm. Where should a point source be placed between the lens and the miror, so that the light, after getting reflected by the mirror and then getting transmitted by the lens, comes out parallel to the principal axis?
View SolutionA source of light is located at double focal length from a convergent lens. The focal length of the lens is f=30cm. At what distance from the lens should a flat mirror be placed, so that the rays reflected from the mirror are parallel after passing through the lens for the second time?
View Solution
