Velocity Of Approach
Step by step video & image solution for Velocity Of Approach by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Two particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m//s, their centre of mass has a velocity of 0.5 m/s. When the relative velocity of approach becomes 3 m/s. When the relative velocity of approach becomes 3m/s, the velocity of the centre of mass is 0.75 m/s.
View SolutionTwo particles of masses m1 and m2 initially at rest a infinite distance from each other, move under the action of mutual gravitational pull. Show that at any instant therir relative velocity of approach is √2G(m1+m2)/R where R is their separation at that instant.
View Solution
Knowledge Check
Two particles of mass m and M are initially at rest and infinitely separated from each other. Due to mutual interaction, they approach each other.
Their relative velocity of approach at a separation d between them, isA[2 GdM + m]1/2B[2 G(M+m)d]1/2C2 GM+mdDNone of theseAssertion :− velocity time graph of two paticles undergoing head−on collison is shown in the figure. If collision is inelastic then value of y must be less than x.

Reason :− Coefficient of restitution(e)=|velocity of separation||velocity of approach|AIf both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.BIf both Assertion & Reason are True but Reason is not a correct explanation of the Assertiion.CIf Assertion is True but the Reason is False.DIf both Assertion & Reason are FalseThese questions consists of two statements each printed as Assertion and Reason. While answering these question you are required to choose any one of the following five responses.
Reason: For inelastic collision, 0≤e<1. Hence, the magnitude of relative velocity of separation after collision is less than relative velocity of approach before collision.AIf both Assertion and Reason are correct and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.CIf Assertion is true but Reason is false.DIf Assertion is false but Reason is true.
Two bodies of mass m1andm2 are initially at rest placed infinite distance apart. They are then allowed to move towards each other under mutual gravitational attaction. Show that their relative velocity of approach at separation r betweeen them is
v=√2G(m1+m2)r
View SolutionTwo particles of mass 'm' and 3 m are initially at rest an infinite distance apart. Both the particles start moving due to gravitational attraction. At any instant their relative velocity of approach is íGmd where 'd' is their separation at that instant. Find ne.
View SolutionA body of mass m moving with a velocity v is approaching a second object of same mass but at rest. The kinetic energy of the two objects as viewed from the centre of mass is
View SolutionComprehension # 2
When two bodies collide normally they exert equal and opposite impulses on each other. Impulse = change in linear momentum. Coefficient of restitution between two bodies is given by :-
e=|Relative velocity of separation||Relative velocity of approach|=1, for elastic collision

Two bodies collide as shown in figure. During collision they exert impulse of magnitude J on each other.
For what value of J (in N−s ) the 2kg block will change its direction of velocity :-
View SolutionComprehension # 2
When two bodies collide normally they exert equal and opposite impulses on each other. Impulse = change in linear momentum. Coefficient of restitution between two bodies is given by :-
e=|Relative velocity of separation||Relative velocity of approach|=1, for elastic collision
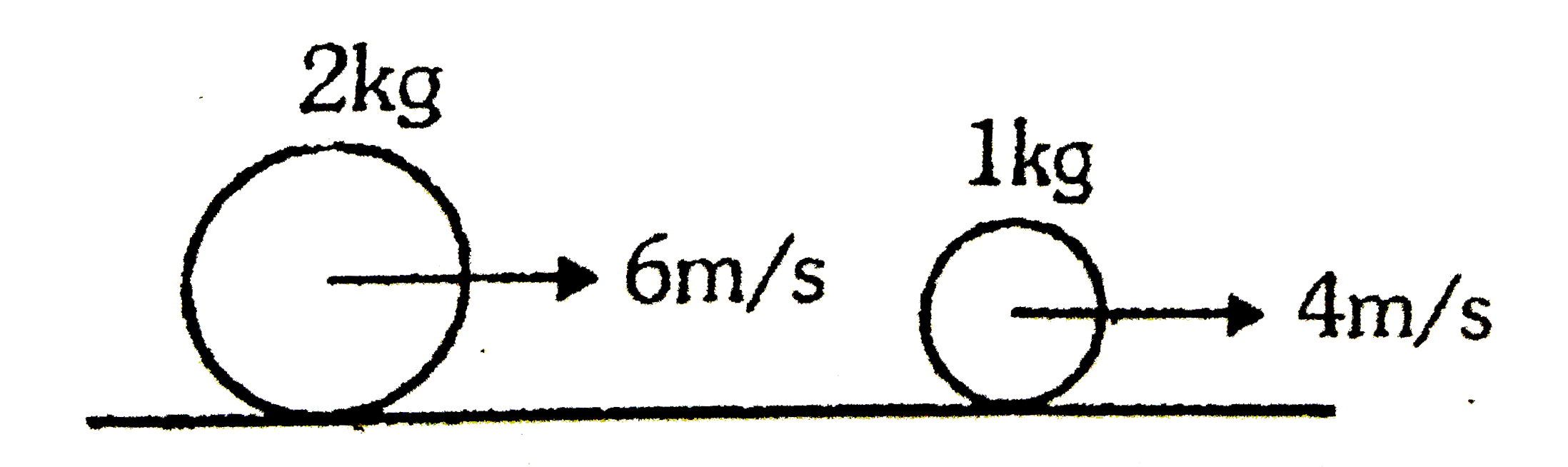
Two bodies collide as shown in figure. During collision they exert impulse of magnitude J on each other.
If the collision is elastic, the value of J is ............. N−s :-
View Solution
