Most Probable Velocity
Step-by-Step Solution for Most Probable Velocity
1. Understanding the Concept:
- The most probable speed (V_mp) is defined as the speed possessed by the maximum fraction of the total number of molecules in a gas. This means that among all the molecules in a gas, the most probable speed is the one that is most frequently observed.
2. Example Illustration:
- Consider a sample of gas molecules. For instance, if we have 10 molecules with varying speeds, we can observe that some molecules share the same speed.
- If we list their speeds, we might find:
- 1 m/s: 1 molecule
- 2 m/s: 2 molecules
- 3 m/s: 4 molecules
- 4 m/s: 1 molecule
- 5 m/s: 1 molecule
- In this case, the speed that is possessed by the maximum number of molecules is 3 m/s, which means V_mp = 3 m/s.
3. Formula for Most Probable Speed:
- The formula for calculating the most probable speed in an ideal gas is given by:
Vmp=√2RTM
- Where:
- R is the gas constant (8.314 J/(mol·K)),
- T is the absolute temperature in Kelvin,
- M is the molar mass of the gas in kg/mol.
4. Alternate Formulation:
- The most probable speed can also be expressed using Boltzmann's constant (k):
Vmp=√2kTm
- Where:
- k is Boltzmann's constant (1.38 x 10^-23 J/K),
- T is the absolute temperature in Kelvin,
- m is the mass of a single gas molecule.
5. Conclusion:
- The most probable speed gives us insight into the behavior of gas molecules at a given temperature and is essential for understanding kinetic theory.
- The most probable speed (V_mp) is defined as the speed possessed by the maximum fraction of the total number of molecules in a gas. This means that among all the molecules in a gas, the most probable speed is the one that is most frequently observed.
- Consider a sample of gas molecules. For instance, if we have 10 molecules with varying speeds, we can observe that some molecules share the same speed.
- If we list their speeds, we might find:
- 1 m/s: 1 molecule
- 2 m/s: 2 molecules
- 3 m/s: 4 molecules
- 4 m/s: 1 molecule
- 5 m/s: 1 molecule
- In this case, the speed that is possessed by the maximum number of molecules is 3 m/s, which means V_mp = 3 m/s.
- The formula for calculating the most probable speed in an ideal gas is given by:
Vmp=√2RTM
- Where:
- R is the gas constant (8.314 J/(mol·K)),
- T is the absolute temperature in Kelvin,
- M is the molar mass of the gas in kg/mol.
- The most probable speed can also be expressed using Boltzmann's constant (k):
Vmp=√2kTm
- Where:
- k is Boltzmann's constant (1.38 x 10^-23 J/K),
- T is the absolute temperature in Kelvin,
- m is the mass of a single gas molecule.
- The most probable speed gives us insight into the behavior of gas molecules at a given temperature and is essential for understanding kinetic theory.
Similar Questions
Match the following:
Column-IColumn-II(A) Root mean square velocity(p)√3Pd(B) Average velocity(q)√3RTm(C) Most probable velocity(r)√8Pπd(D) Velocity possessed by maximum fraction of molecules(s)√2RTm
View SolutionDetermine the gas temperature at which
(a) the root mean square velocity of hydrogen molecules exceeds their most probable velocity by Δv=400m/s ,
(b) the velocity distribution function F(v) for the oxygen molecules will have the maximum value at the velocity v=420m/s.
View Solution
Knowledge Check
The ratio of most proble velocity to that of average velocity is
Aπ2B2πC√π2D2√π
Most probable structure of P isA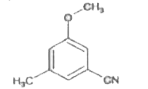 B
B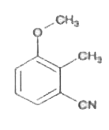 C
C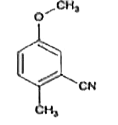 Dnone of the above
Dnone of the aboveThe most probable product in the following reaction is :
 A
A B
B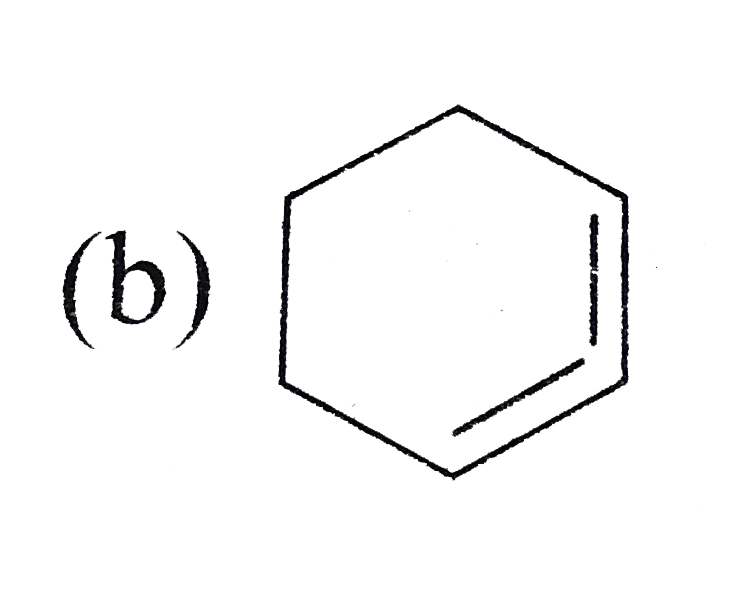 C
C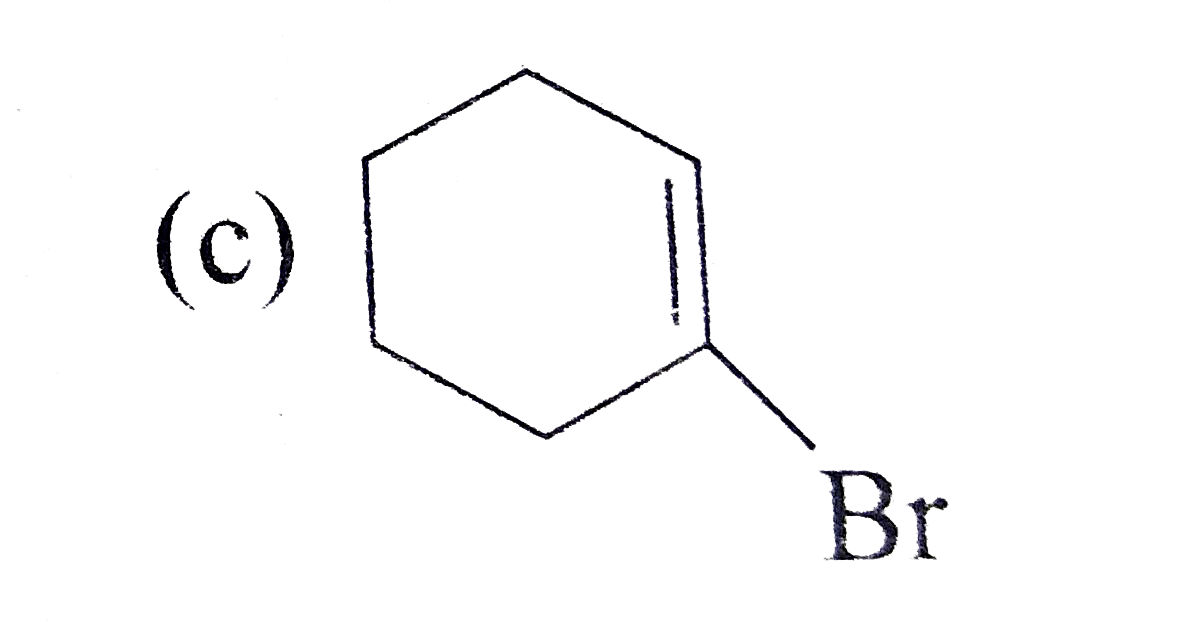 D
D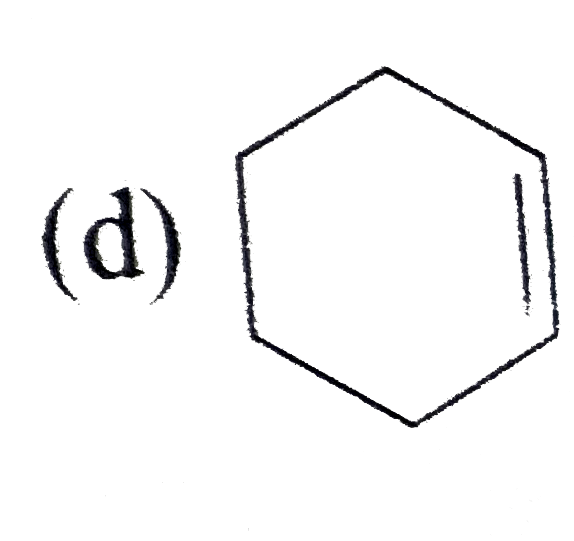
Assume a sample of an ideal gas in a vessel. The velocities of molecules in the sample are between 2ms to 5ms. If the velocity of molecules (v) and the number of molecules (n) are related as n=7y−v2−10, then the most probable velocity (in ms ) in the sample is (Here v is measured in ms ).
View SolutionAt what temperature of a nitrogen and oxygen mixture do the most probable velocities of nitrogen and oxygen molecules differ by Δv=30m/s ?
View SolutionMost Probable Speed
View SolutionThe most probable product in the following reaction is :
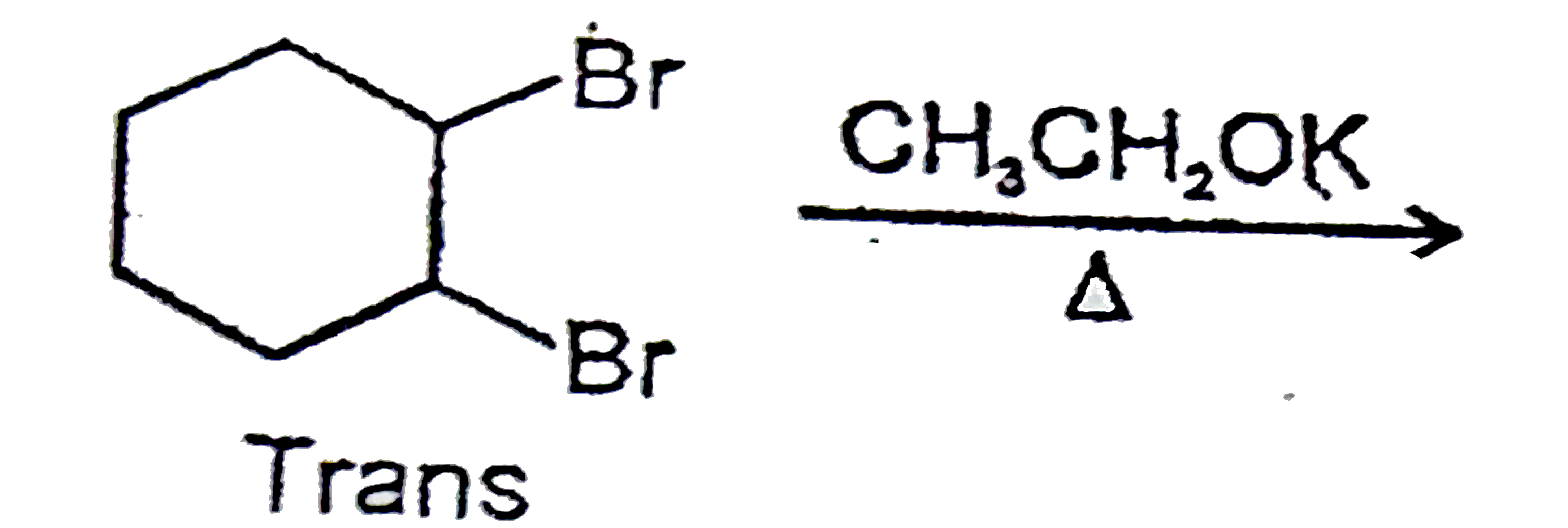
View SolutionIn the following reaction the most probable product will be :
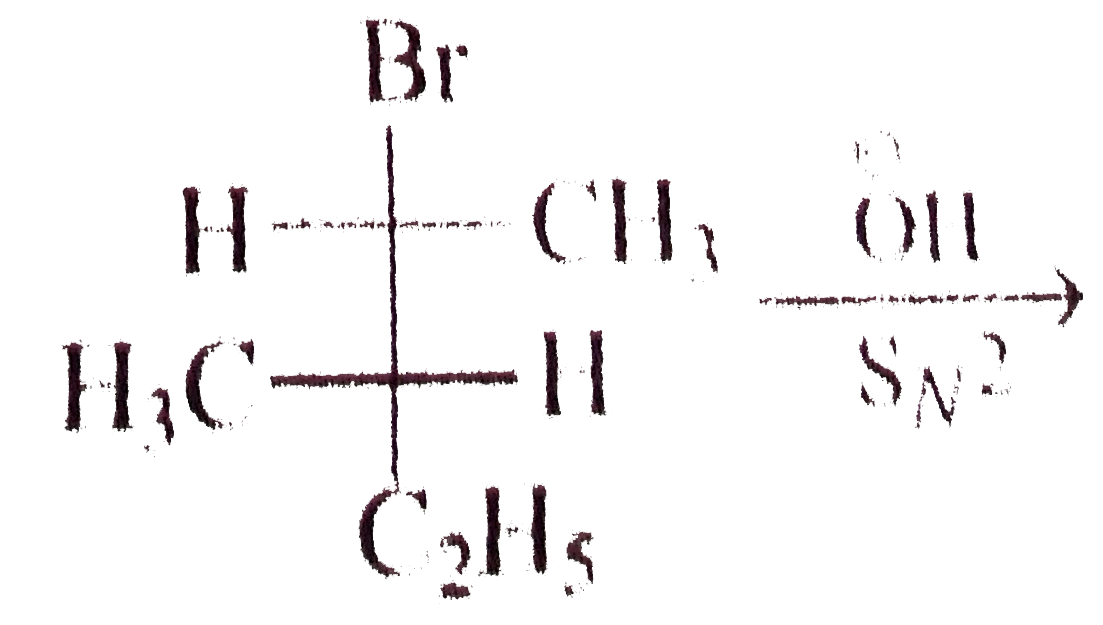
View Solution
