OSCILLATION OF A LIQUID COLUMN IN U-TUBE
Step by step video & image solution for OSCILLATION OF A LIQUID COLUMN IN U-TUBE by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
STATEMENT-1 : The height of a liquid column in a U-tube is 0.3m. If the liquid in one of the limbs is depressed, and then released, the time period of liquid column will be 1.1sec.
STATEMENT-2 : this follows from the relation.
T=2π√hgAStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.A U-tube having a liquid of density ρ is accelerated at a m/s2 , so as to create be the height difference between two columns of l/2 (as shown if figure) . If/is the length of the base of U-tube the value of acceleration given to the system is
 A4.9m/s2B9.8m/s2C5.6m/s2D6.4m/s2
A4.9m/s2B9.8m/s2C5.6m/s2D6.4m/s2
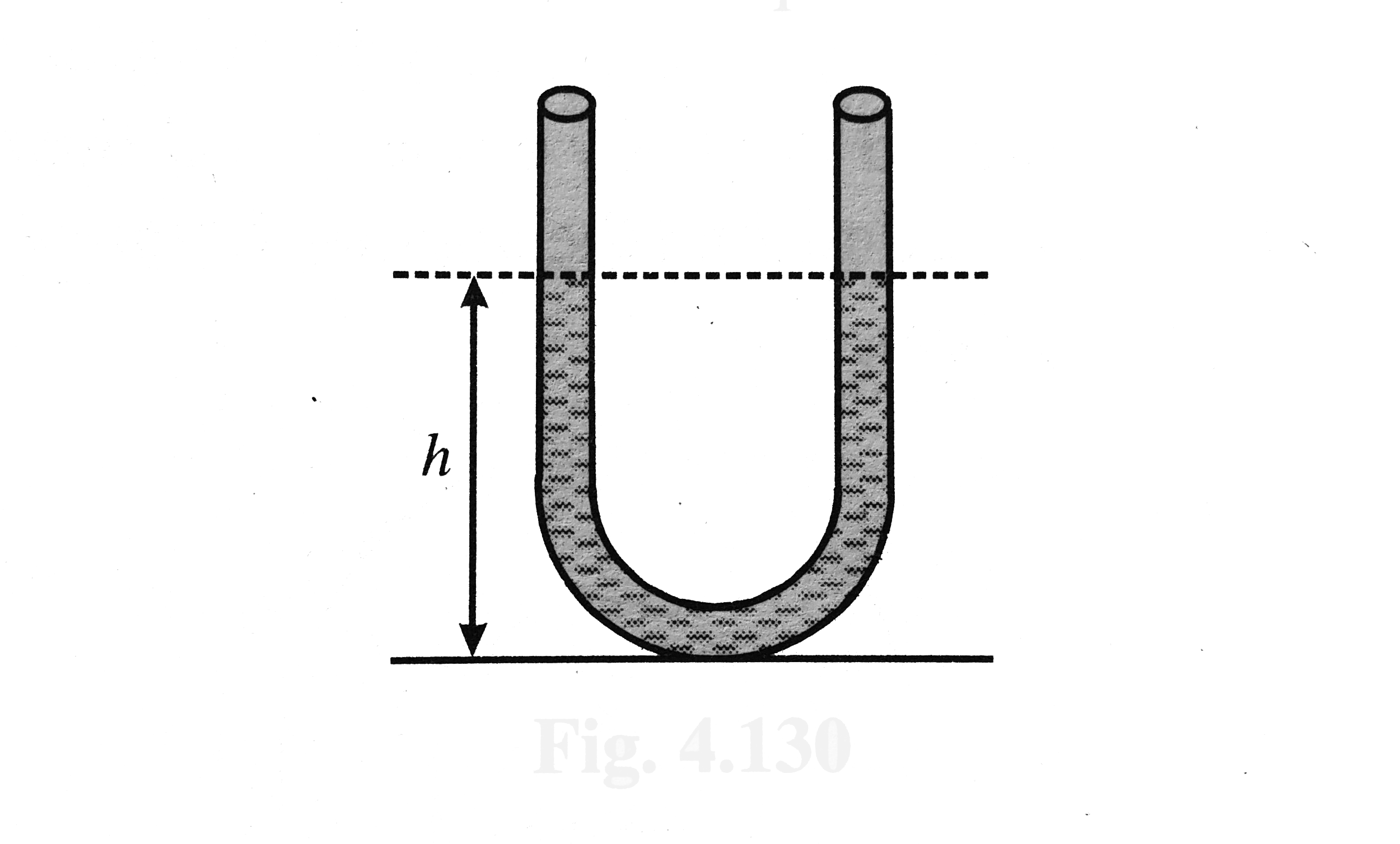
Consider a liquid which fills a uniform U - tube uniform U- tube, as shown in figure , up to a height h. Find angular the frequency of small oscillation of th eliquid in the U - tube.
View SolutionSTATEMENT-1: Time period of the liquid executing S.H.M.in a U-tube depends on the area of cross section of U-tube.
and
STATEMENT-2 : The restoring force acting on liquid displaced from equilibrium position of U -tube depends on the difference in levels of liquid in the two limbs of U -tube.
View SolutionHydrostatics: Pressure due to a Liquid Column | Equating pressure in U-tube Problems | Force and Torque on container wall (point of application of force)
View SolutionSHM in spring pulley system | SHM of liquid in U tube | Block on liquid surface | Angular SHM Kinematics | Dynamics of angular SHM | Simple pendulum
View SolutionIn the given table, Column I gives type of oscillation, Column II gives change in amplitude of oscillation and Column III gives examples of these types of oscillation.

The combination that defines the features of free oscillation is
View SolutionIn the given table, Column I gives type of oscillation, Column II gives change in amplitude of oscillation and Column III gives examples of these types of oscillation.

The combination that defines the features of damped oscillation is
View Solution
