POSITION , SIZE AND NATURE OF IMAGE FORMED BY SPHERICAL MIRRORS
To determine the position, size, and nature of the image formed by spherical mirrors (both concave and convex), we can use the mirror formula and the characteristics of ray diagrams. Here’s a step-by-step solution:
Step 1: Understand the Mirror Formula
The mirror formula is given by:
1f=1u+1v
where:
- f = focal length of the mirror
- u = distance of the object from the mirror (taken as negative for real objects in concave mirrors)
- v = distance of the image from the mirror
Step 2: Identify the Type of Mirror
Determine whether you are working with a concave or convex mirror. The nature of the image will differ based on the type of mirror used.
Step 3: Draw Ray Diagrams
For accurate analysis, draw ray diagrams for both concave and convex mirrors:
- Concave Mirror:
- Draw a ray parallel to the principal axis, which reflects through the focal point.
- Draw a ray through the focal point, which reflects parallel to the principal axis.
- Draw a ray striking the mirror at the pole, reflecting according to the law of reflection.
- Convex Mirror:
- Draw a ray parallel to the principal axis, which reflects as if it is coming from the focal point behind the mirror.
- Draw a ray directed towards the focal point, which reflects parallel to the principal axis.
- Draw a ray striking the mirror at the pole, reflecting according to the law of reflection.
Step 4: Determine the Position of the Image
Using the ray diagrams:
- For a concave mirror:
- If the object is beyond the center of curvature (C), the image is real, inverted, and smaller than the object.
- If the object is at C, the image is real, inverted, and the same size as the object.
- If the object is between C and the focal point (F), the image is real, inverted, and larger than the object.
- If the object is at F, the image is formed at infinity.
- If the object is between F and the mirror, the image is virtual, upright, and larger than the object.
- For a convex mirror:
- The image is always virtual, upright, and smaller than the object, regardless of the object's position.
Step 5: Calculate the Size of the Image
The magnification (m) can be calculated using the formula:
m=h′h=−vu
where:
- h′ = height of the image
- h = height of the object
- m = magnification (positive for upright images, negative for inverted images)
Step 6: Nature of the Image
- Concave Mirror:
- Real images are inverted and can be projected on a screen.
- Virtual images are upright and cannot be projected.
- Convex Mirror:
- Always forms virtual images that are upright and smaller.
Conclusion
By applying the mirror formula and analyzing the ray diagrams, we can determine the position, size, and nature of the image formed by spherical mirrors.
---
The mirror formula is given by:
1f=1u+1v
where:
- f = focal length of the mirror
- u = distance of the object from the mirror (taken as negative for real objects in concave mirrors)
- v = distance of the image from the mirror
Determine whether you are working with a concave or convex mirror. The nature of the image will differ based on the type of mirror used.
For accurate analysis, draw ray diagrams for both concave and convex mirrors:
- Concave Mirror:
- Draw a ray parallel to the principal axis, which reflects through the focal point.
- Draw a ray through the focal point, which reflects parallel to the principal axis.
- Draw a ray striking the mirror at the pole, reflecting according to the law of reflection.
- Convex Mirror:
- Draw a ray parallel to the principal axis, which reflects as if it is coming from the focal point behind the mirror.
- Draw a ray directed towards the focal point, which reflects parallel to the principal axis.
- Draw a ray striking the mirror at the pole, reflecting according to the law of reflection.
Using the ray diagrams:
- For a concave mirror:
- If the object is beyond the center of curvature (C), the image is real, inverted, and smaller than the object.
- If the object is at C, the image is real, inverted, and the same size as the object.
- If the object is between C and the focal point (F), the image is real, inverted, and larger than the object.
- If the object is at F, the image is formed at infinity.
- If the object is between F and the mirror, the image is virtual, upright, and larger than the object.
- The image is always virtual, upright, and smaller than the object, regardless of the object's position.
The magnification (m) can be calculated using the formula:
m=h′h=−vu
where:
- h′ = height of the image
- h = height of the object
- m = magnification (positive for upright images, negative for inverted images)
- Concave Mirror:
- Real images are inverted and can be projected on a screen.
- Virtual images are upright and cannot be projected.
- Convex Mirror:
- Always forms virtual images that are upright and smaller.
By applying the mirror formula and analyzing the ray diagrams, we can determine the position, size, and nature of the image formed by spherical mirrors.
Similar Questions
Knowledge Check
The nature of image formed by a plane mirror is
Avirtual and erectBof the same size as the objectClaterally invertedDall the above are correct
Introduction|Light Travels In A Straigth Line|Image Forming By Plane Mirror|Spherical Mirror|Dispersion Of Light|OMR
View SolutionImage Formation By Spherical Mirror
View SolutionLight|Various Phenomena Of Light|Reflection|Properties Of The Image Formed By A Plane Mirror|Spherical Mirrors|OMR
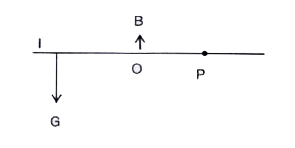
View SolutionIn the figure given below, OB is the object and IG is the image formed. A spherical mirror with P as the pole of the mirror is used to form image IG. Identify the type of spherical mirror used and also locate the position of focus of the mirror using the ray diagram.
View SolutionVelocity OF image in Spherical mirror
View SolutionImage Formation by Spherical Mirrors
View SolutionImage Formation by Spherical Mirrors
View Solution
