Theorem 7.3 : The sides opposite to equal angles of a triangle are equal.
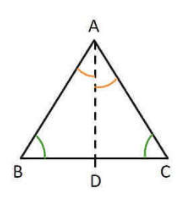
In △BAD and △CAD
∠B=∠C (given)
∠BAD=∠CAD
AD=AD (common)
By AAS congruence rule, △BADand △CAD are congruent. Thus,
AB=AC
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 7.41videos
NCERT THEOREMS
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 7.51videos
NCERT THEOREMS
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 7.21videos
NCERT THEOREMS
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES8videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.42videos
NUMBER SYSTEMS
Similar Questions
Angles opposite to two equal sides of a triangle are equal.
View SolutionWhich of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600. If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View Solution
Knowledge Check
- Question 1 - Select One
The side opposite to an obtuse angle of a triangle is :
AsmallestBgreatestChalf of the perimeterDnone of these - Question 2 - Select One
Which of the following is false?
(A) The sum of any two sides of a triangle is equal to the third side.
(B) The sum of the exterior angles of a triangle is equal to 360∘AA and BBOnly ACOnly BDNone of these
Fill the blanks in the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are ......
(ii) Angle opposite to equal sides of a triangle are .....
(iii) In an equilateral triangle all angles are .....
(iv) In a ΔABC if ∠A = ∠C , then AB = ......
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = ....
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……View SolutionTheorem 7.2 : Angles opposite to equal sides of an isosceles triangle are equal.
View SolutionProve that the angle opposite to the equal sides of an equilateral triangle are equal.
View SolutionAngles opposite to two equal sides of a triangle are equal. GIVEN : ABC in which AB=AC TO PROVE : ∠C=∠B CONSTRUCTION : Draw the bisector AD of ∠A which meets BC in D Figure
View SolutionThe angles opposite to equal sides of an isosceles triangle are ..........
View SolutionIf the angles of a triangle are in the ratio 2:3:7, then the sides opposite to the angles are in the ratio
View Solution

