Prove that a diagonal of a parallelogram divides it into two congruent triangles.
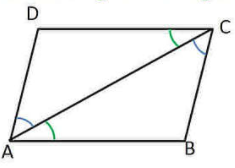
opposites sides of parallelogram are parallel. Thus
So, AB∣∣DC and AD∣∣BC.
In △ABC and △ADC,
∠BAC=∠DCA
AC=AC (common)
∠DAC=∠BCA
Thus, with ASA congruency, △ABC and △ADC are congruent.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 8.21videos
NCERT THEOREMS
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 8.31videos
NCERT THEOREMS
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 7.81videos
NCERT THEOREMS
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES8videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.42videos
NUMBER SYSTEMS
Similar Questions
Knowledge Check
- Question 1 - Select One
Prove that each of the following diagonals of a parallelogram divides it into two congurent triangles. The following lowing are the steps involved in proving the above results. Arrange them in sequential order.
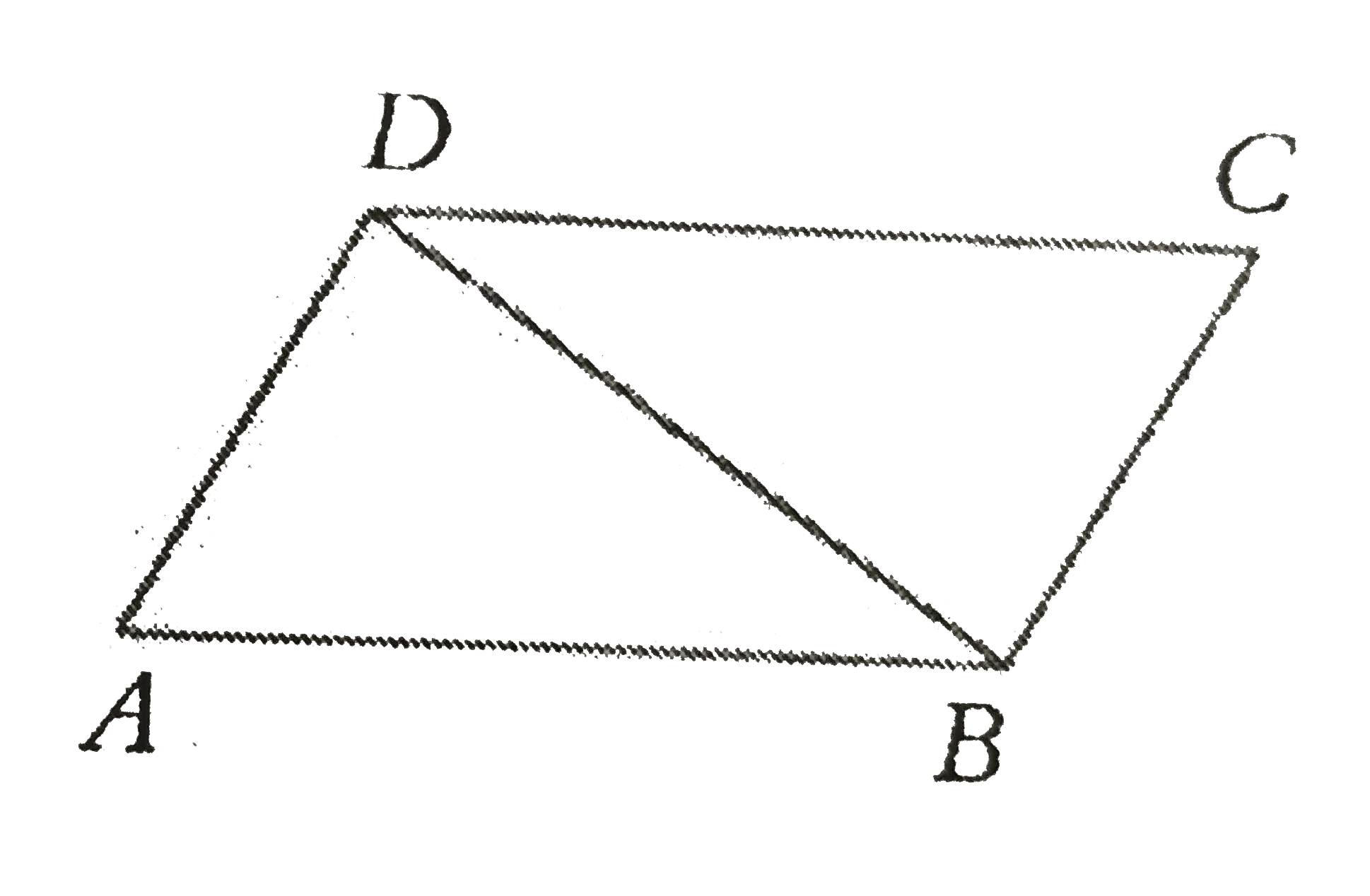
(A) By SSS conguruence property , ΔDAB≅ΔBCD.
(B) Let ABCD be a parallelogram and join BD.
(C ) AB=CD,AD=BC(opposite sides of parallelogram) and BD=BD (common side).
(D ) Similarly , AC divides the parallelogram into two congruent triangles.AABCDBBCADCBACDDCBAD
Prove that each of the following diagonals of a parallelogram divides it into two congurent triangles. The following lowing are the steps involved in proving the above results. Arrange them in sequential order.

(A) By SSS conguruence property , ΔDAB≅ΔBCD.
(B) Let ABCD be a parallelogram and join BD.
(C ) AB=CD,AD=BC(opposite sides of parallelogram) and BD=BD (common side).
(D ) Similarly , AC divides the parallelogram into two congruent triangles.View SolutionA diagonal of a parallelogram divides it into two triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area. GIVEN : A parallelogram ABCD . The diagonals AC and BD intersect at O. TO PROVE : ar(OAB)=ar(OBC)=ar(OCD)=ar(AOD)
View SolutionA diagonal of a parallelogram divides it into two triangles of equal area. GIVEN : A parallelogram ABCD in which BD is one of the diagonals. TO PROVE : ar (ABD)=ar(CDB)
View Solution

