State and prove that :
Theorem 10.1 : Equal chords of a circle subtend equal angles at the centre
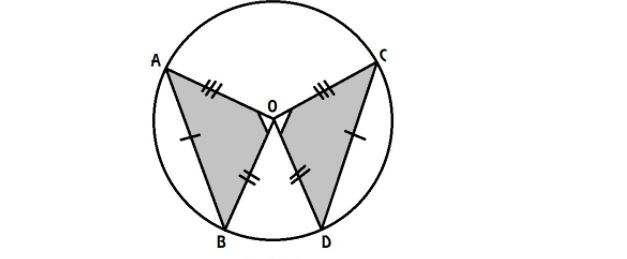
This theorem states that, if there are 2 equal chords in a circle, the angles formed by the equal chords at the center of the circle are equal.
Given
AB and CD are two equal chords in a circle with center O.
To Prove
∠AOB=∠COD
Proof
ConsiderΔAOB and ΔCOD
AO=OC [radii of the same circle]
BO=OD [radii of the same circle]
AB=CD [Given]
∴ ΔAOB≅ΔCOD by SSS congruency.
∠AOB=∠COD [CPCT]
Hence Proved.
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.21videos
NCERT THEOREMS
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.31videos
NCERT THEOREMS
- BOOK - NCERTCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 9.31videos
NCERT THEOREMS
- BOOK - NCERTCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES8videos
LINES AND ANGLES
- BOOK - NCERTCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.42videos
NUMBER SYSTEMS
Similar Questions
Knowledge Check
- Question 1 - Select One
What is the length of the chord of a unit circle which subtends an angle at the centre ?
Asin(θ2)Bcos(θ2)C2sin(θ2)D2cos(θ2)
Equal chords of congruent circles subtend equal angles at the centre.
View SolutionEqual chords of congruent circles subtend equal angles at the centre.
View SolutionRecall that two circles are congruent if they have the same radii. Prove that equalchords of congruent circles subtend equal angles at their centres.
View SolutionTheorem:-1If two arcs of a circle are congruent ; the corresponding chord are equal and Equal chords of a circle substends equal angles at the centre.
View SolutionEqual chords of a circle are equidistant from the centre.
View Solutionprove that the line joining the mid-point of two equal chords of a circle subtends equal angles with the chord.
View SolutionProve that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
View Solution

