The equations of the circle which pass through the origin and make intercepts of lengths 4 and 8 on the X and Y-axes respectively are

A

$x^{2} + y^{2} + 4 x \pm 8 y = 0$

B

$x^{2} + y^{2} + 2 x \pm 4 y = 0$

C

$x^{2} + y^{2} + 8 x \pm 16 y = 0$

D

$x^{2} + y^{2} y \pm x + y = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

In $Δ O A C, o c^{2} = 2^{2} + 4^{2} = 20$
required equation of circle is $< b r >$ (+-2)^(2)+(y+-)^(2)=20 rArr x^(2)+y^(2)+-4x+- 8y=0

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE AND CONICS

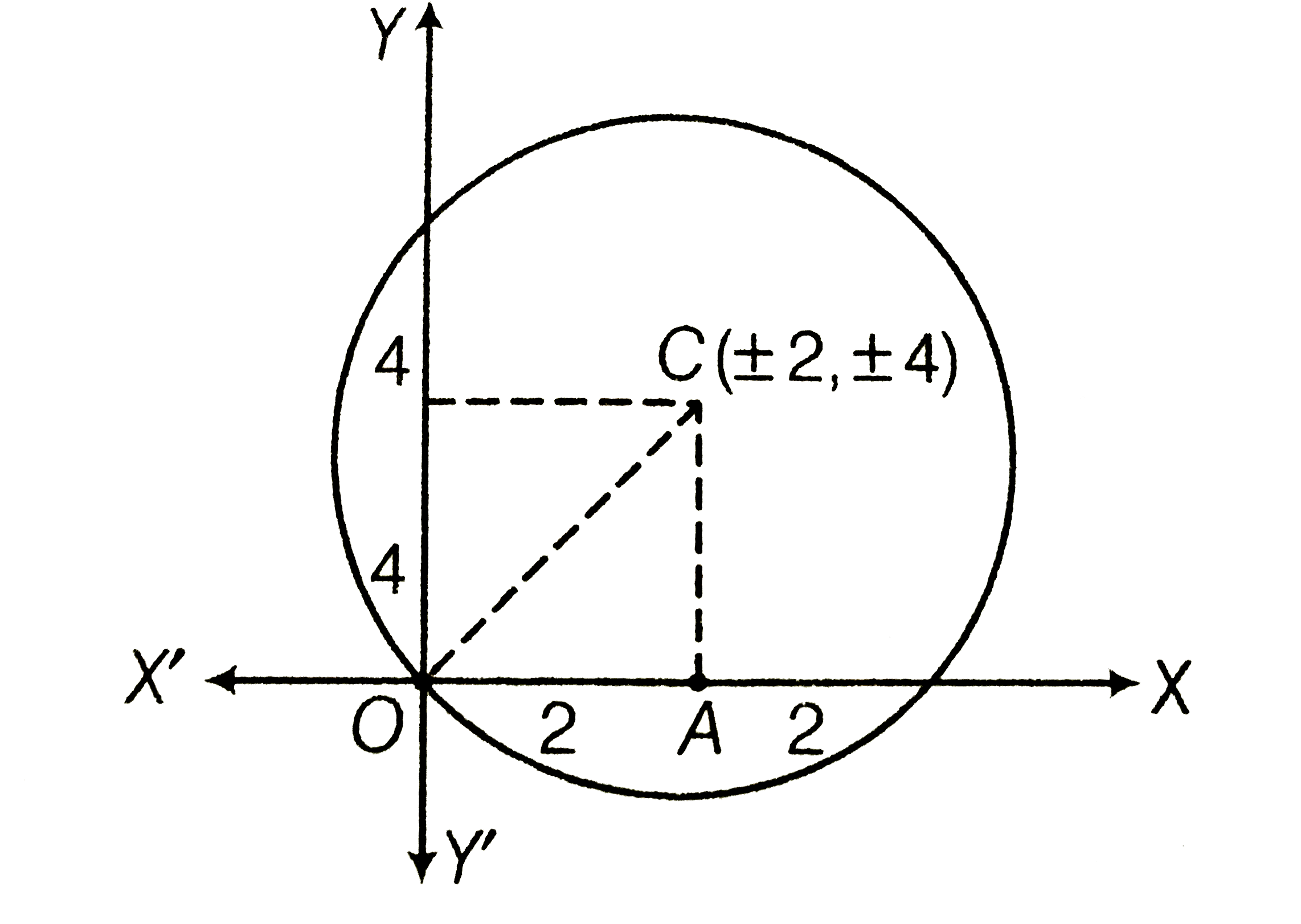
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The equation of the circle which passes through the origin and cuts off intercepts 3 and 4 from the positive of the axes, respectively is
A $4 x^{2} + 12 x y + 4 y^{2} - 16 y = 0$
B $x^{2} + y^{2} - 3 x - 4 y = 0$
C $4 x^{2} - 12 x y + 4 y^{2} + 16 y = 0$
DNone of the above
Question 2 - Select One
The equation of the circle passing through (0, 0) and making intercepts 2 units and 3 units on the x-axis and y-axis repectively, is
A $x^{2} + y^{2} - 6 x - 2 y = 0$
B $x^{2} + y^{2} - 2 x - 3 y = 0$
C $x^{2} + Y^{2} - 2 x - 6 y + 1 = 0$
D $x^{2} + y^{2} - 6 x - 2 y + 2 = 0$
Question 3 - Select One
Equation of the circle through the origin and making intercepts of 3 and 4 on the positive sides of the axes is
A $x^{2} + y^{2} + 3 x + 4 y = 0$
B $x^{2} + y^{2} - 3 x - 4 y = 0$
C $x^{2} + y^{2} + 3 x - 4 y = 0$
D $x^{2} + y^{2} - 3 x + 4 y = 0$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-CIRCLE AND CONICS-All Questions

Home
Ask Doubt
Profile