Calculation Of Energy And Radius
To calculate the energy and radius of an electron in a hydrogen-like atom using Bohr's theory, we can follow these steps:
Step 1: Understand the Formulas
We need to use the formulas derived from Bohr's theory:
1. Energy of the electron in the nth orbit:
En=−2.18×10−18J⋅z2n2
2. Radius of the nth orbit:
Rn=52.9×n2zpm
Where:
- En is the energy of the electron,
- Rn is the radius of the nth orbit,
- z is the atomic number,
- n is the principal quantum number.
Step 2: Determine the Values of z and n
For a hydrogen atom, the atomic number z=1. Choose a value for n (for example, n=1 for the ground state).
Step 3: Calculate the Energy
Substituting the values into the energy formula:
En=−2.18×10−18⋅1212=−2.18×10−18J
Step 4: Calculate the Radius
Substituting the values into the radius formula:
Rn=52.9×121=52.9pm
Step 5: Summary of Results
For a hydrogen atom in the ground state (n=1):
- Energy E1=−2.18×10−18J
- Radius R1=52.9pm
We need to use the formulas derived from Bohr's theory:
1. Energy of the electron in the nth orbit:
En=−2.18×10−18J⋅z2n2
2. Radius of the nth orbit:
Rn=52.9×n2zpm
- En is the energy of the electron,
- Rn is the radius of the nth orbit,
- z is the atomic number,
- n is the principal quantum number.
For a hydrogen atom, the atomic number z=1. Choose a value for n (for example, n=1 for the ground state).
Substituting the values into the energy formula:
En=−2.18×10−18⋅1212=−2.18×10−18J
Substituting the values into the radius formula:
Rn=52.9×121=52.9pm
For a hydrogen atom in the ground state (n=1):
- Energy E1=−2.18×10−18J
- Radius R1=52.9pm
Similar Questions
Bohr Model OF Atom || Calculation OF Radius OF Orbit || Calculation OF velocity OF electron in orbit || Calculation OF Energy OF Electron in Orbit
View SolutionQuestions|Important Postulates Of Niels Bohr Atomic Theory|Mathematical Interpretation Of BMA|Calculation Of Radius & Energy Levels Of Hydrogen Atom|Calculation Of Radius Of Bohr's Orbit|The Velocity Of Electron In Bohr's Stationary Orbits|Total Energy Of Electron In Bohr's Stationary Orbits|Merits Of Bohr's Theory|Some Important Terms Related To Energy|Questions|OMR
View SolutionLimiting radius ratio|Calculation of limiting radius ratio for different voids
View SolutionA mercury drop of radius R is sprayed into n droplets of equal size. Calculate the energy expanded if surface tension of mercury is T.
View SolutionCalculate the energy and momentum of a photon of wavelength 6600Å
View SolutionCalculate the amount of energy evolved when eight drplets of mercury (surface tension 0.55Nm−1) of radius 1 mm each combine into one.
View SolutionRecap |Energy Calculation|Examples|Energy Diagram|Hydrogen Atom|Hydrogen Spectrum|Rydberg Formula For Calculating Any Wavelength|OMR
View SolutionCalculate the energy stored in the condenser the given circuit
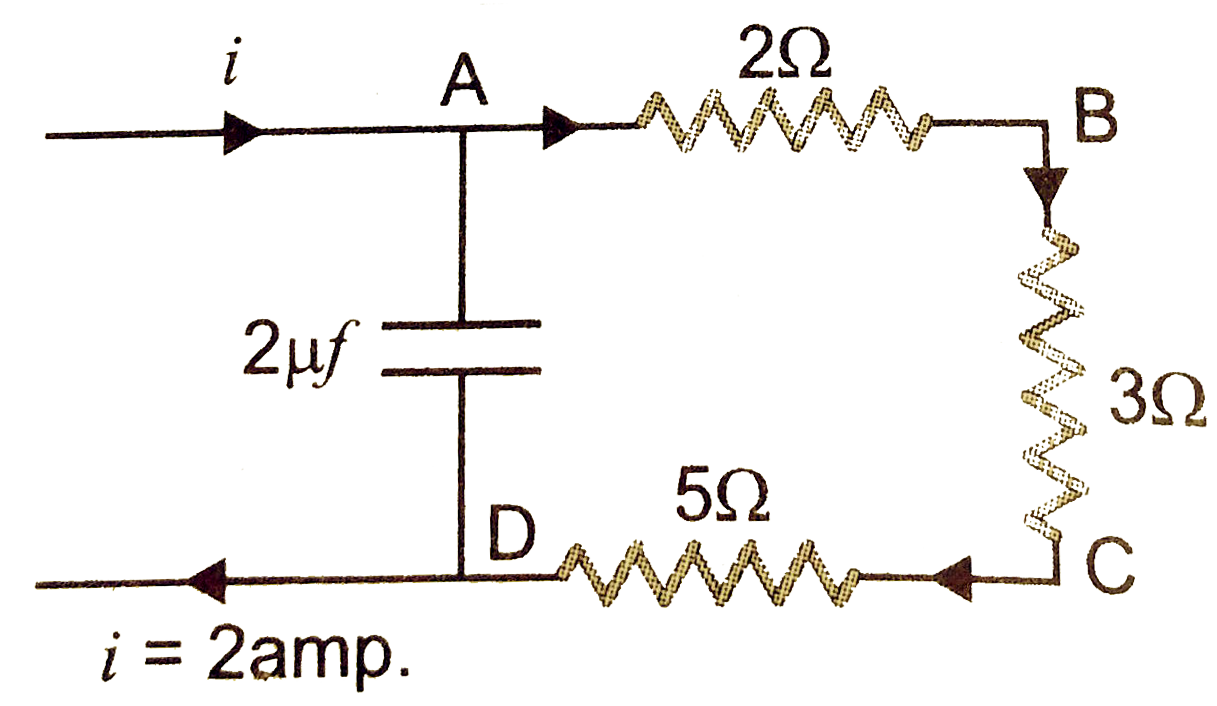
View SolutionCalculate potential energy of a magnetic dipole in a magnetic field.
View SolutionState the formula for calculating energy transferred by heat.
View Solution
