If sinA=2√5andcosB=1√10 where A and B are acute angles , then what is A +B equal to ?
A
135∘
B
90∘
C
75∘
D
60∘
Text Solution
The correct Answer is:A
Given , sinA=2√5andcosB=2√10
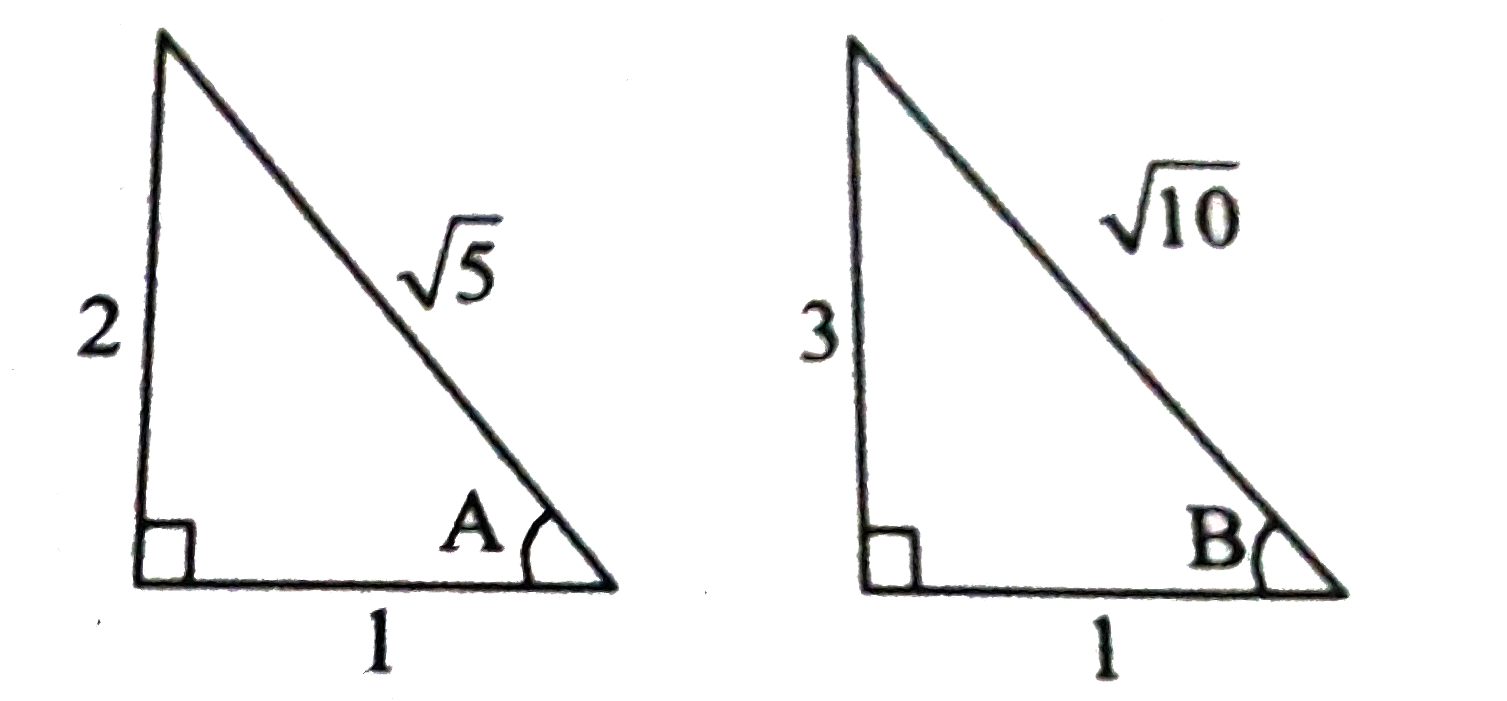
∴cosA=1√5sinB=3√10
∴sin(A+B)=sincosB+cosAsinB
=(2√15)(1√10)+(1√5)(3√10)
=2√50+3√50=5√50=5√25×2=55√2=1√2
sin(A+B)=1√2⇒sin(90+45)=1√2
(∵sin(90+45)=cos45∘)
∴A=90∘andB=45∘
∴A+B=90∘+45∘=135∘
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If sinA=1√10andsinB=1√5, where A and B are positive acute angles, then A+B=?
AπBπ2Cπ4Dπ3If sinA=1√10 and sinB=1√5, where A and B are positive acute angles, then A+B is equal to
AπBπ2Cπ3Dπ4If sin A = 1/√5, cos B = 3/√10, A, B being positive acute angles, then what is (A + B) equal to ?
Aπ/6Bπ/4Cπ/3Dπ/2
Let sin(A+B)=√32andcosB=√32, where A, B are acute angles. What is tan(2A−B) equal to ?
View SolutionIf A and B are acute angles and sinA=cosB then A+B=
View SolutionIf sinA=35, and A is an acute angle, then tanA+secA is equal to:
View SolutionIf sinAsinB=√32andcosAcosB=√52,0<A,B<π2, then tanA−tanB is equal to
View SolutionIf 3−2√56−√5=a+b√c where a and b are rational numbers, then what are the values of a and b ?
View Solution
