Two integers xandy are chosen with replacement out of the set {0,1,,2,3,10}. Then find the probability that |x−y|>5.
611
35121
30121
25121
The correct Answer is:C
Probability =2×12×5×611×11=30121.
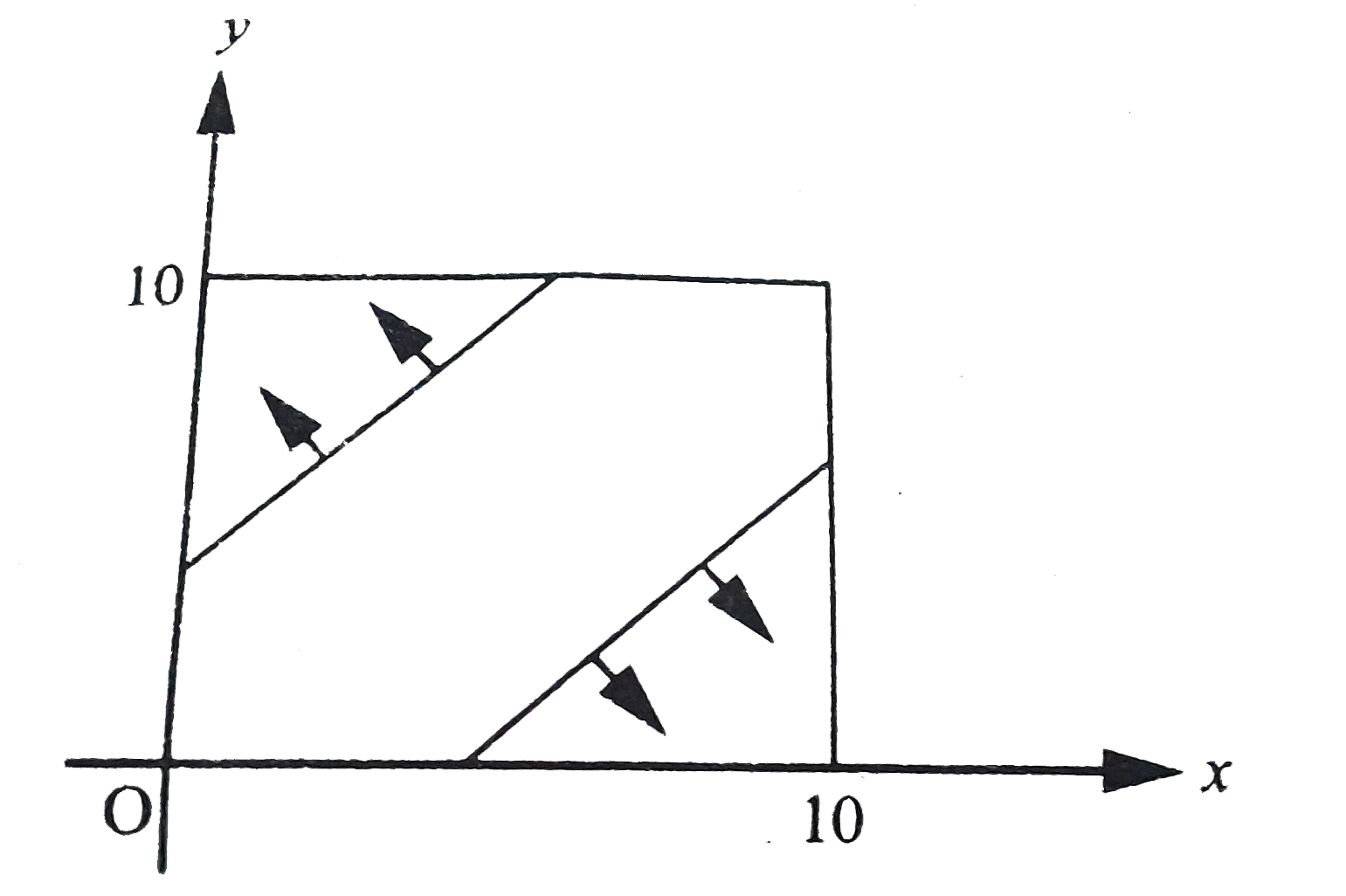 .
.
Topper's Solved these Questions
- POLYNOMIAL,QUADRATIC EQUATION & INEQUALITIESBOOK - NDA PREVIOUS YEARSCHAPTER - POLYNOMIAL,QUADRATIC EQUATION & INEQUALITIESEXERCISE - Math
170 Videos
- PROPERTIES OF TRIANGLE, INVERSE TRIGONOMETRIC FUNCTIONBOOK - NDA PREVIOUS YEARSCHAPTER - PROPERTIES OF TRIANGLE, INVERSE TRIGONOMETRIC FUNCTIONEXERCISE - MCQ
103 Videos
Similar Questions
Knowledge Check
Two integers x and y are chosen with replacement out of the set {0, 1, 2, 3, ... 10). Then the probability that |x - y । > 5 is:
A711B40121C35121D30121Two integers xandy are chosen with replacement out of the set {0,1,,2,3,10}. Then find the probability that |x−y|>5.
A711B40121C35121D30121Two integers x and y are chosen with replacement out of the set {0, 1, 2, . . . 10}. The probability that |x - y| doesn't exceed 5 is
A511B81121C311D91121
Two integers xandy are chosen (with replacement) at random from {x:0≤x≤10,x is an integer). If the probability for |x−y|≤5 is p, then the value of 121p13 is
View SolutionIf two distinct numbers m and n are chosen at random form the set {1, 2, 3, …, 100}, then find the probability that 2m+2n+1 is divisible by 3.
View SolutionTwo numbers xandy are chosen at random (without replacement) from among the numbers 1,2,3,2004. The probability that x3+y3 is divisible by 3 is (a) 13 (b) 23 (c) 16 (d) 14
View SolutionIf a and b and c are 3 numbers not necessarily different chosen randomly and with replacement from the set {1,2,3,4,5}, then the probability that ab+c is even is
View SolutionTwo integers x and y are chosen with replacement out of the set {0, 1, 2, 3, ... 10). Then the probability that |x - y । > 5 is:
View Solution
