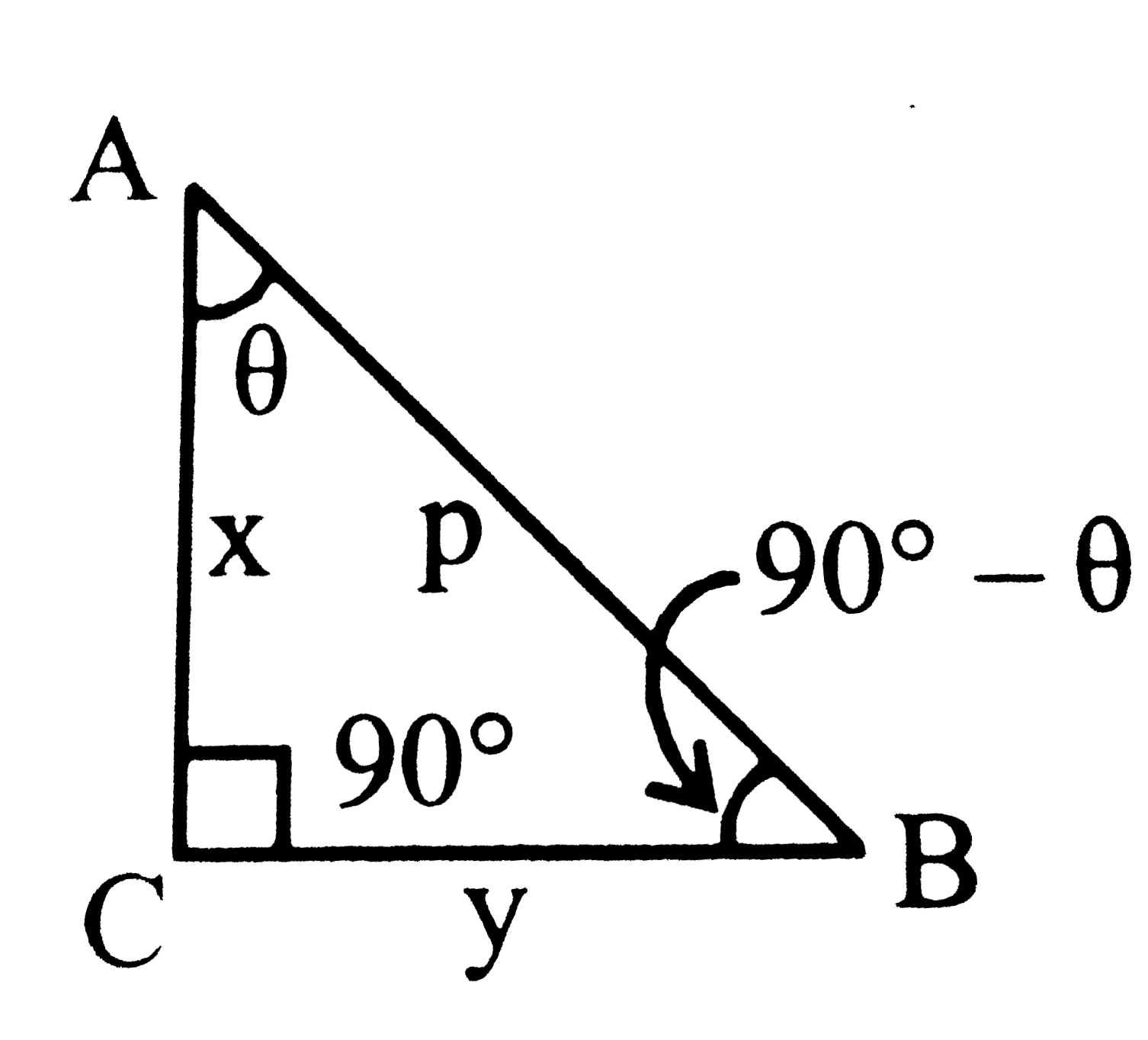
If in a right-angled triangle ABC, hypotenuse AC=p, then what is −−→AB.−−→AC+−−→BC.−−→BA+−−→CA.−−→CB equal to ?
A
P, Q, R are the vertices of an equilateral triangle
B
p2
C
2p2
D
p22
Video Solution
Text Solution
The correct Answer is:B
−−→AB.−−→AC+−−→BC.−−→BA+−−→CA.−−→CA
=(AB.AC.cosθ)+(BC.BA.cos(90−θ))+(CA.CB.cos90)
=(p.x.cosθ)+(y.p.sinθ)+0
=p[xcosθ+ysinθ]
By projection formula:
p=xcosθ+ycos(90−θ)
=xcosθ+ysinθ
∴p[xcosθ+ysinθ]=p×p=p2.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a right angled triangle ABC, the hypotenuse AB =p, then −−→AB.−−→AC+−−→BC.−−→BA+−−→CA.−−→CB is equal to:
A2p2Bp22Cp2DNone of theseIn a right angled triangle hypotenuse AC= p, then −−→AB.−−→AC+−−→BC.−−→BA+−−→CA.−−→CB equal to ?
Ap2B2p2Cp22DpIf ABCDE is a pentagon, then
−−→AB+−−→AE+−−→BC+−−→DC+−−→ED+−−→AC is equal toA4−−→ACB2−−→ACC3−−→ACD5−−→AC
In a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
View SolutionABCDE is a pentagon prove that −−→AB+−−→BC+−−→CD+−−→DE+−−→EA=→0
View SolutionABCD is a parallelogram . If −−→AB=→a,−−→BC=→b, then what −−→BD equal to ?
View SolutionIn a triangle ABC, if taken in order, consider the following statements:
1.−−→AB+−−→BC+−−→CA=→0
2. −−→AB+−−→BC−−−→CA=→0
3. −−→AB−−−→BC+−−→CA=→0
4. −−→BA−−−→BC+−−→CA=→0
How many of the above statements are correct?
View SolutionIf A, B, C and D are four points in space having ∣∣∣−−→AB×−−→CD+−−→BC×−−→AD+−−→CA×−−→BD∣∣∣, then the value = k (Area of △ABC) of k is equal to
View Solution
