If f(x)= Min {|x−1|,|x|,|x+1|}then∫1−1f(x)dx eqals
A
1
B
2
C
0
D
none of these
Video Solution
Text Solution
The correct Answer is:D
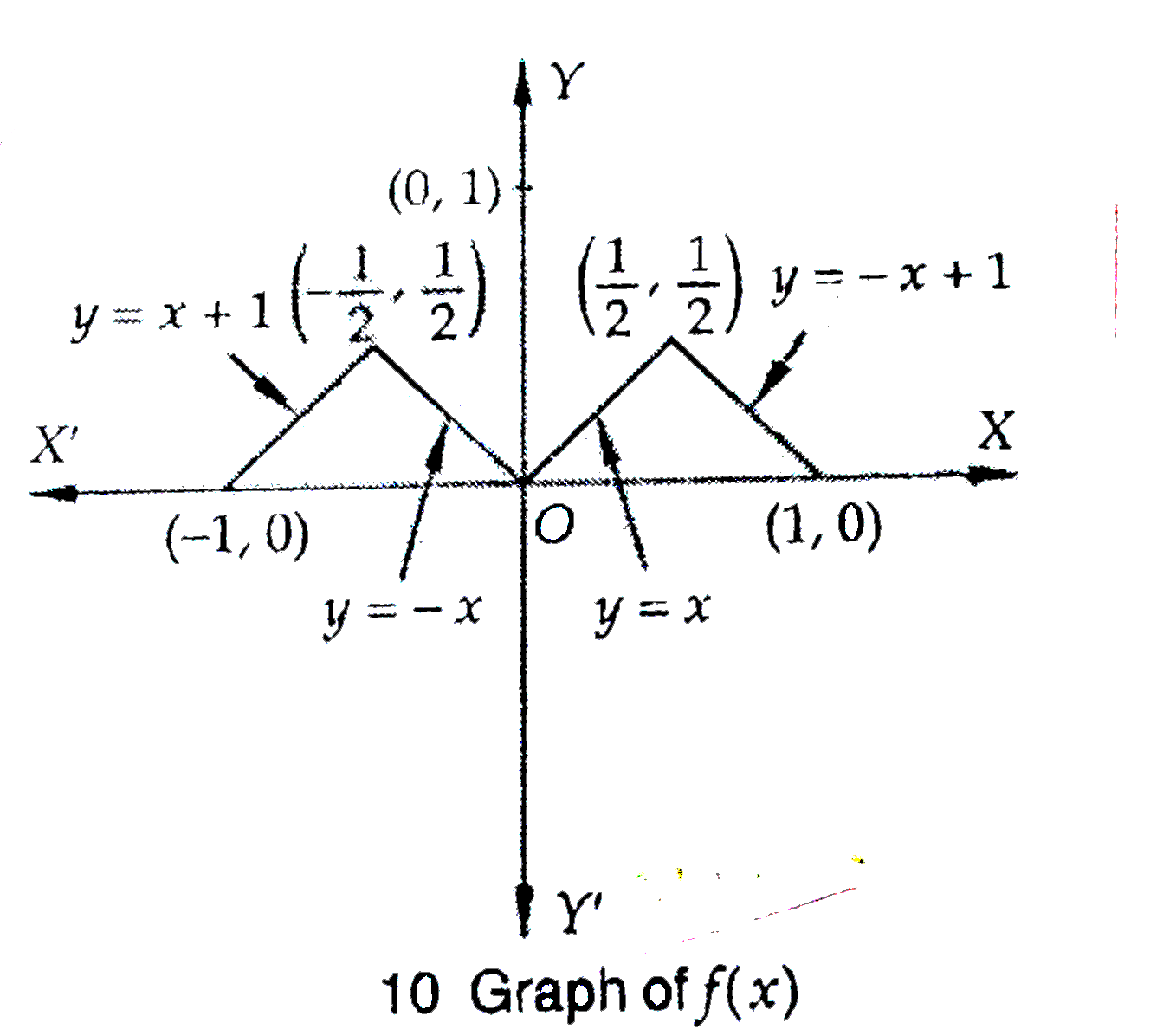
The graph of f(x) is as shown in Fig. 10.
1∫−1f(x)dx=21∫−1f(x)dx=2(12×1×12)=12
|
Topper's Solved these Questions
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Section II - Assertion Reason Type
12 Videos
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Exercise
147 Videos
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 2
60 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
86 Videos
- DERIVATIVE AS A RATE MEASURER BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise
26 Videos
Similar Questions
Knowledge Check
If ∫1−1f(x)dx=0 then
Af(−x)=f(x)Bf(−x)=−f(x)Cf(x)=2f(x)Df(−x)=2f(x)if f(x)=|x−1| then ∫20f(x)dx is
A1B0C2D-2If 2f(x)−3f(1/x)=x, then ∫21f(x)dx is equal to
A(3/5)log2B(−3/5)(1+log2)C(−3/5)log2DNone of these
f(x)=|2x−1|+|x−1|, then ∫2−2f(x)dx= ……
View SolutionLet f(x) be maximum and g(x) be minimum of (x|x|,x2|x|} then ∫1−1[f(x)−g(x)]dx=
View SolutionLet f(x)=min[x+1,√1−x], then ∫1−1f(x)dx is
View Solutionf(x)=min{2sinx,1−cosx,1} then ∫π0f(x)dx is equal to
View SolutionLet f(x) be maximum and g(x) be minimum of {x|x|,x2|x|} then ∫1−1[f(x)−g(x)]dx=
View Solution
