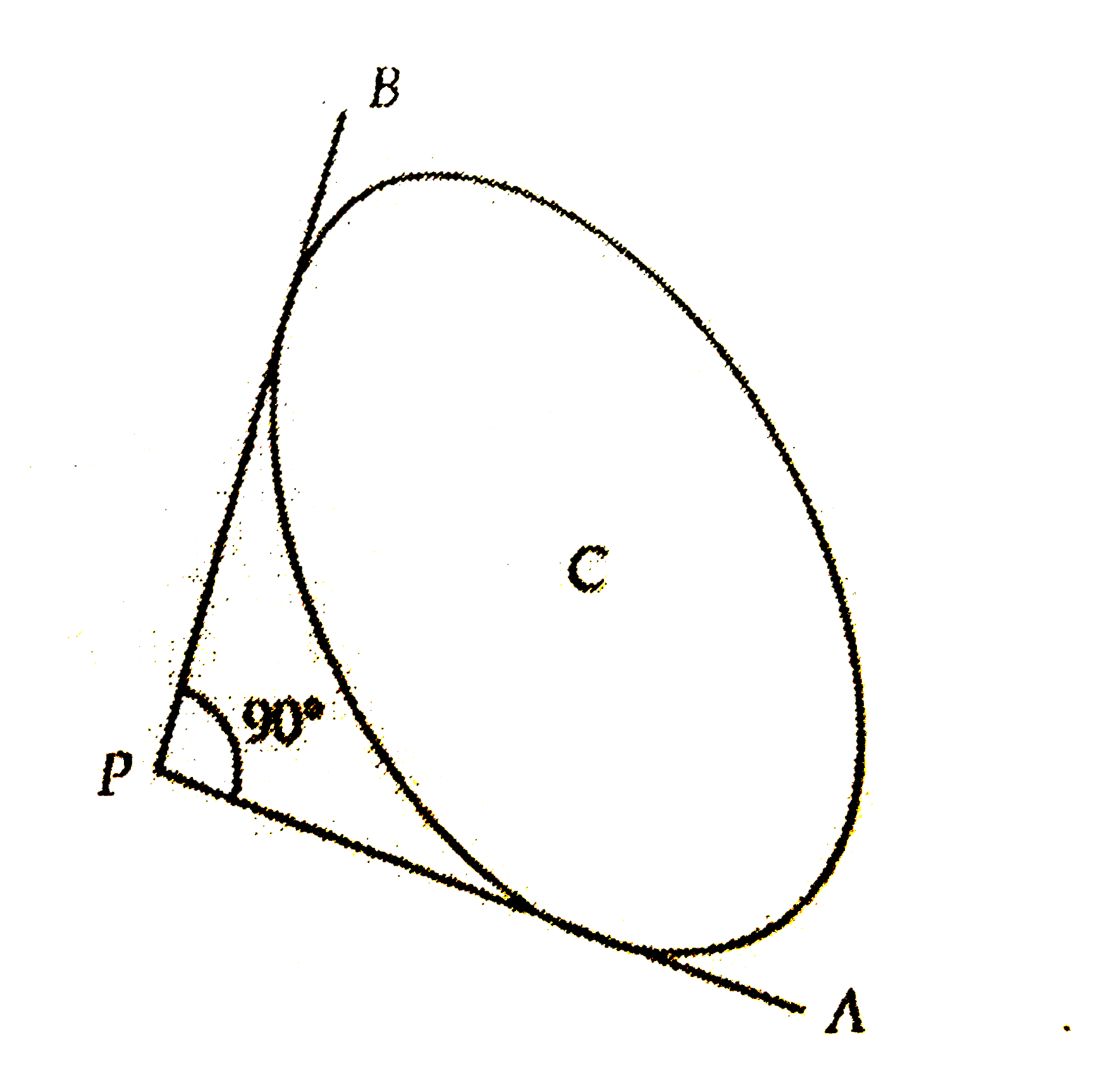
An ellipse slides between two perpendicular straight lines. Then identify the locus of its center.
parabola
ellipse
hyperbola
circle
The correct Answer is:D
Clearly, P is the point of intersection of perpendicular tangents. So, P lies on the director circle of the given ellipse x2a2+y2b2=1 (say). This means that the centre of the ellipse will always remain at a constant distance √a2+b2 from P. Hence, the locus of C is a circle.
Topper's Solved these Questions
- ELLIPSEBOOK - OBJECTIVE RD SHARMACHAPTER - ELLIPSEEXERCISE - Section II - Assertion Reason Type
7 Videos
- ELLIPSEBOOK - OBJECTIVE RD SHARMACHAPTER - ELLIPSEEXERCISE - Exercise
82 Videos
- ELLIPSEBOOK - OBJECTIVE RD SHARMACHAPTER - ELLIPSEEXERCISE - Chapter Test
30 Videos
- DIFFERENTIATIONBOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIATIONEXERCISE - Chapter Test
30 Videos
- EXPONENTIAL AND LOGARITHMIC SERIESBOOK - OBJECTIVE RD SHARMACHAPTER - EXPONENTIAL AND LOGARITHMIC SERIESEXERCISE - Chapter Test
20 Videos
Similar Questions
A line of fixed length a+b moves so that its ends are always on two fixed perpendicular straight lines. Then the locus of the point which divides this line into portions of length aandb is a/an ellipse (b) parabola straight line (d) none of these
View SolutionA rod of length l slides with its ends on two perpendicular lines. Find the locus of its midpoint.
View Solution
Knowledge Check
An ellipse slides between two perpendicular lines the locus of its centre , is
AcircleBparabolaCellipseDhyperbolaAn ellipse slides between two perpendicular lines the locus of its centre , is
Aa circleBan ellipseCa parabolaDa pair of straight linesIf the extremities of a line segment of length l moves in two fixed perpendicular straight lines, then the locus of the point which divides this line segment in the ratio 1 : 2 is-
Aa parabolaBan ellipseCa hyperbolaDNone of these
A circle cuts two perpendicular lines so that each intercept is of given length. The locus of the centre of the circle is conic whose eccentricity is
View SolutionA stick of length l slides with its ends on two mutually perpendicular lines. Find the locus of the middle point of the stick.
View SolutionRelation "perpendicular" in the straight lines in a plane is :
View SolutionA circle passes through a fixed point A and cuts two perpendicular straight lines through A in B and C. If the straight line BC passes through a fixed-point (x1,y1), the locus of the centre of the circle, is
View SolutionA circle touches a given straight line and cuts off a constant length 2d from another straight line perpendicular to the first straight line. The locus of the centre of the circle, is
View Solution
