Let , be the end points of the latus rectum of the ellipse . The equations of parabolas with latus rectum PQ are
The correct Answer is:B
We have,
Let e be the eccentricity of this ellispe. Then,
Clearly, coordinates of P and Q are and respectively.
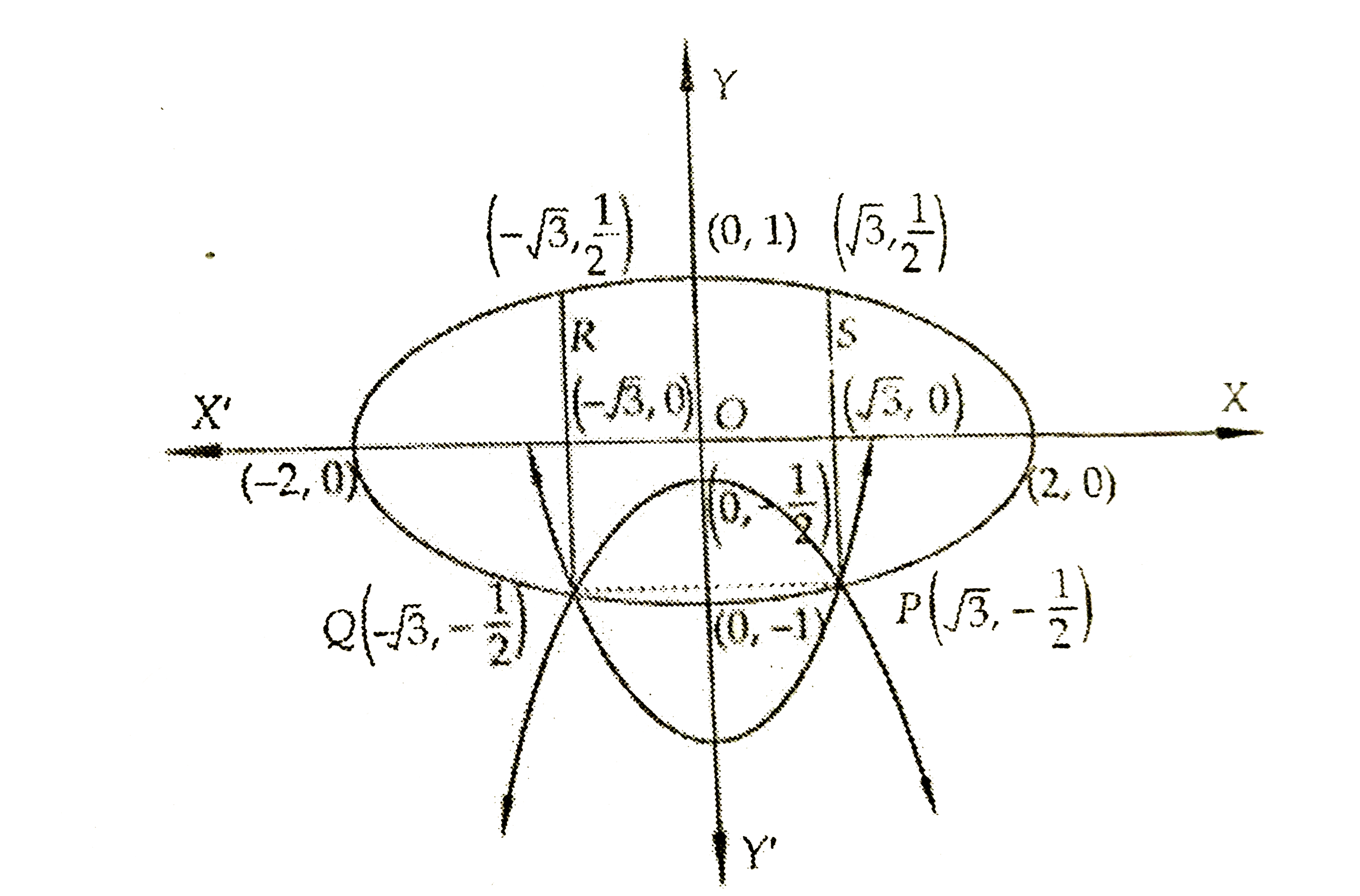
Latusrectum of the parabola
Cooridnates of foci of two parabolas are and .
So, the coordinates of the vertices of two parabola are
Hence, their equations are
or and
Topper's Solved these Questions
- ELLIPSEBOOK - OBJECTIVE RD SHARMACHAPTER - ELLIPSEEXERCISE - Section II - Assertion Reason Type
7 Videos
- ELLIPSEBOOK - OBJECTIVE RD SHARMACHAPTER - ELLIPSEEXERCISE - Exercise
82 Videos
- ELLIPSEBOOK - OBJECTIVE RD SHARMACHAPTER - ELLIPSEEXERCISE - Chapter Test
30 Videos
- DIFFERENTIATIONBOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIATIONEXERCISE - Chapter Test
30 Videos
- EXPONENTIAL AND LOGARITHMIC SERIESBOOK - OBJECTIVE RD SHARMACHAPTER - EXPONENTIAL AND LOGARITHMIC SERIESEXERCISE - Chapter Test
20 Videos
Similar Questions
Knowledge Check
For points P≡(x1,y1) and Q≡(x2,y2) of the coordinates plane, a new distance d (P,Q) is defined by d(P,Q)=|x1−x2|+|y1−y2|. Let O≡(0,0) and A≡(3,2). Consider the set of points P in the first quadrant which are equidistant (with respect to the new distance) from O and A.
The area of the ragion bounded by the locus of P and the line y=4 in the first quadrant isA2sq.unitsB4 sq.unitsC6 sq.unitsDnoen of theseFor points P≡(x1,y1) and Q≡(x2,y2) of the coordinates plane, a new distance d (P,Q) is defined by d(P,Q)=|x1−x2|+|y1−y2|. Let O≡(0,0) and A≡(3,2). Consider the set of points P in the first quadrant which are equidistant (with respect to the new distance) from O and A.
The set of poitns P consists ofAone straight line onlyBunion of two line segmentsCunion of two infinite raysDunion of a line segment of finite length and an infinite rayFor points P≡(x1,y1) and Q≡(x2,y2) of the coordinates plane, a new distance d(P,Q) is defined by d(P,Q)=|x1−x2|+|y1−y2|. Let O≡(0,0) and A≡(3,2). Consider the set of points P in the first quadrant which are equidistant (with respect to the new distance) from O and A.
The locus of point P isAone -one and onto functionBmany one and onto functionCone-one and into functionDrelation but not function
Let PQ be a line segment with P(x1,y1,z1)andQ(x2,y2,z2) and let L. be a straight line whose d.c.'s are l, m, n. Then the length of projection of PQ on the line L is
View SolutionThe ratio in which the line segment joining P(x1, y1) and Q(x2, y2) is divided by x-axis is y1:y2 (b) y1:y2 (c) x1:x2 (d) x1:x2
View SolutionFor points P=(x1,y1)andQ=(x2,y2) of the coordinate plane, a new distance d(P,Q) is defined by d(P,Q)=|x1−x2|+|y1−y2|. Let O(0,0) and A=(3,2). Prove that the set of points in the first quadrant which are equidistant (wrt new distance) from O and A consists of the union of a line segment of finite length and an infinite ray. Sketch this set in a labelled diagram.
View SolutionIf the line segment joining the points P(x1,y1)and Q(x2,y2) subtends an angle α at the origin O, prove that : OP.OQ cosα=x1x2+y1y2.
View SolutionThe line y=mx+1 touches the curves y=0x4+2x2+x at two points P(x1,y1) and Q(x2,y2). The value of x21+x22+y21+y22 is
View Solution
