If z1,z2,z3 are the affixes of the vertices of a triangle having its circumcenter at the origin. If z is the affix of its orthocenter, then
z1+z2+z3+z=0
z1+z2+z3−z=0
z1−z2+z3+z=0
z1+z2−z3+z=0
The correct Answer is:B
We know that the centroid G, circumference O, and orthocenter O′ of a triangle are collinear such that G divides OO′ in the ratio 1:2. Since, affix of G is z1+z2+z33 and O is the origin.
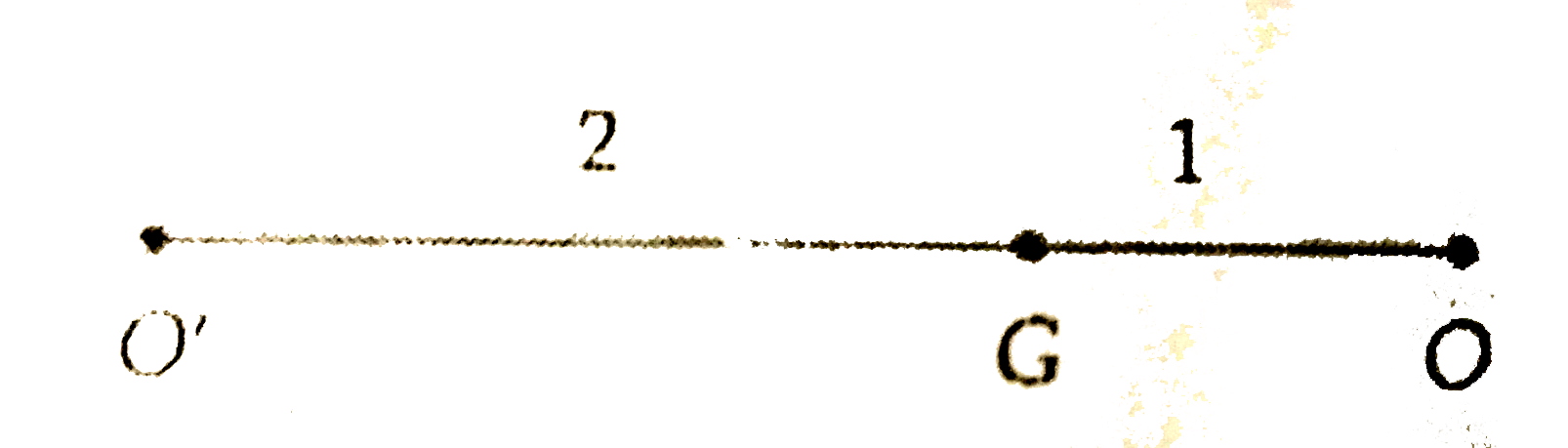
z1+z2+z33=1×z+2×01+2
⇒z=z1+z2+z3⇒z1+z2+z3−z=0
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Section I - Solved Mcqs
141 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
86 Videos
Similar Questions
If z1,z2andz3 are the affixes of the vertices of a triangle having its circumcentre at the
origin. If zis the affix of its orthocentre, prove that
Z1+Z2+Z3−Z=0.
View SolutionIf z1,z2,z3 be the affixes of the vertices A,BMandC of a triangle having centroid at G such ;that z=0 is the mid point of AG then 4z1+Z2+Z3=
View Solution
Knowledge Check
If z1,z2,z3 are the affixes of the vertices of a triangle having its circumcenter at the origin. If z is the affix of its orthocenter, then
Az1+z2+z3−z=0Bz1+z2−z3+z=0Cz1−z2+z3=z=0D−z1+z2+z3+z=0If z1,z2,z3 represent the vertices of a triangle, then the centroid of the triangle is given by
Aaz1+bz2+cz3a+b+cBz1+z2+z33Cz1z2z33Dnone of theseIf z1,z2,z3,z4 are the affixes of the vertices of a parallelogram taken in order in Argand plane, then
Az1+z3=z2+z4Bz1+z2=z3+z4Cz1−z3=z2−z4DNone of these
Find the relation if z1,z2,z3,z4 are the affixes of the vertices of a parallelogram taken in order.
View SolutionIf z1,z2andz3 are the vertices of an equilasteral triangle with z0 as its circumcentre , then changing origin to z0 ,show that z21+z22+z23=0, wherez1,z2,z3, are new complex numbers of the vertices.
View SolutionIf z1,z2,z3 are the vertices of an isoscles triangle right angled at z2, then
View SolutionIf z1,z2,z3 are affixes of the vertices A, B and C respectively of a triangle ABC having centroid at G such that z = 0 is the mid point of AG, then
View SolutionIf z1,z2andz3 represent the vertices of an equilateral triangle such that
View Solution
