The complex number having least positive argument and satisying $| z - 5 i | \leq 3$ , is

A

$12 + 16 i$

B

$\frac{12}{5} + \frac{16 i}{5}$

C

$\frac{16}{5} + \frac{12 i}{5}$

D

$- \frac{12}{5} + \frac{16 i}{5}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

The region represented by $| z - 5 i | \leq 3$ is the region containing all points lying inside or on the circle having center at (0,5) and radius 3. Clearly, the complex number having the least positive argument in this region is the complex number represented by the point of contact of tangent drawn from the origin to the circle.

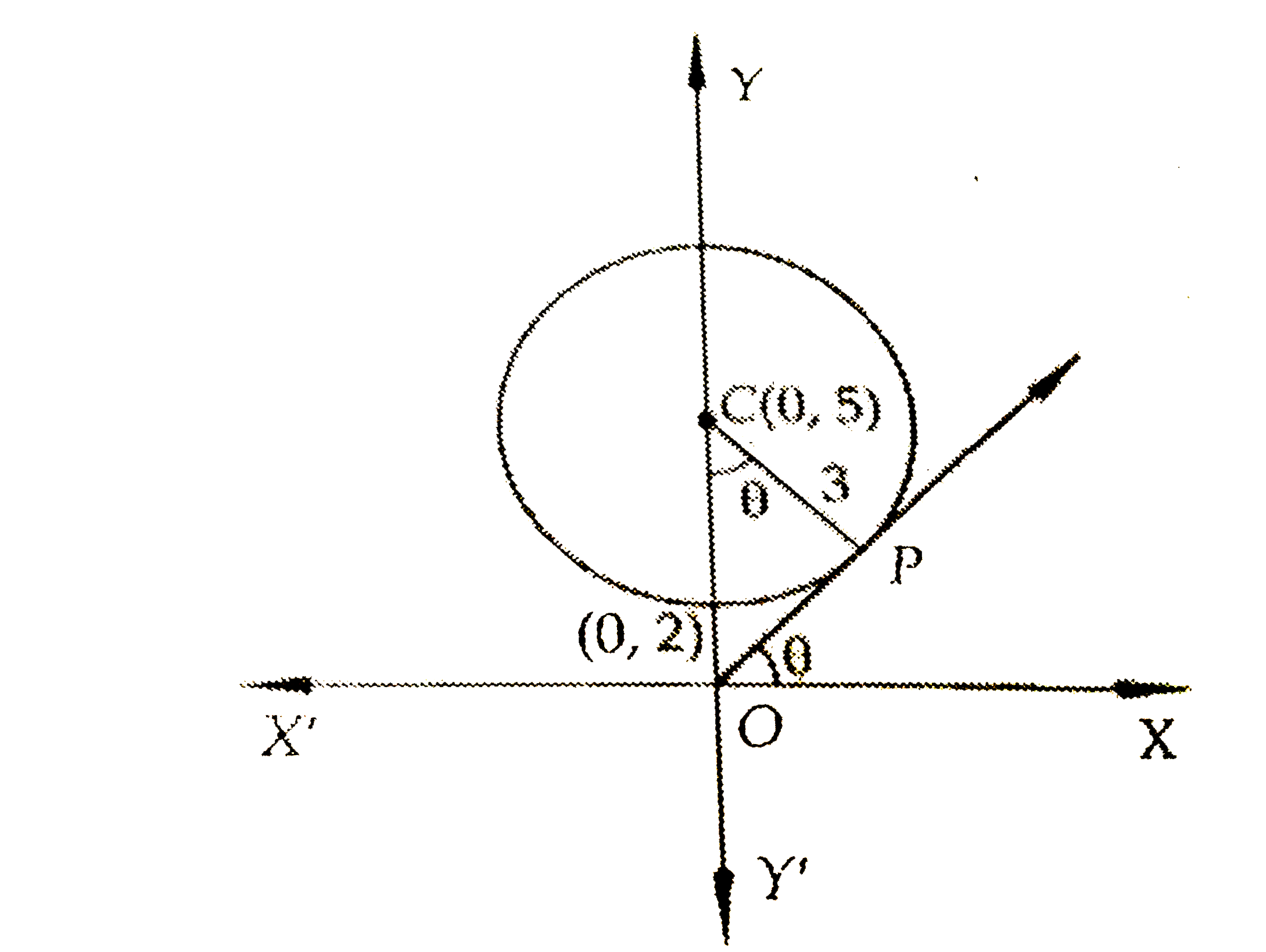
Clearly, $O P = \sqrt{(O C^{2} - C P^{2}) = \sqrt{25 - 9}} = 4$
So, the coordinate of P are $(4 cos θ, 4 sin θ)$ .
From triangle OCP, we have $cos θ = \frac{3}{5}$
So, the coordinates of P are $(12 / 5, 16 / 15)$ .
Hence, required complex number is $\frac{12}{5} + \frac{16}{5} i$ .

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The real part of a complex number z having minimum principal argument and satisfying $| z - 5 i | \leq 1$ is
A $\frac{2}{5} \sqrt{6}$
B0
C $\frac{2}{\sqrt{5}}$
D $- \frac{1}{5} \sqrt{6}$
Question 2 - Select One
If z is a complex number having least absolute value and $| z - 2 + 2 i | = ∣,$ then $z =$
A $(2 - 1 / \sqrt{2}) (1 - i)$
B $(2 - 1 / \sqrt{2}) (1 + i)$
C $(2 + 1 / \sqrt{2}) (1 - i)$
D $(2 + 1 / \sqrt{2}) (1 + i)$
Question 3 - Select One
The real part of the complex number z satisfying $| z - 1 - 2 i | \leq 1$ and having the least positive argument, is
A $\frac{4}{5}$
B $\frac{8}{5}$
C $\frac{6}{5}$
D $\frac{7}{5}$

OBJECTIVE RD SHARMA-COMPLEX NUMBERS -Chapter Test

Home
Ask Doubt
Profile