The population growth is generally described by the following equation : dNdt=rN(K−NK) What does 'r' represent in the given equation ?
To answer the question about what 'r' represents in the population growth equation dNdt=rN(K−NK), we can break it down step by step:
1. Understanding the Equation: The equation dNdt=rN(K−NK) describes how a population changes over time. Here, N represents the current population size, K is the carrying capacity of the environment, and t is time.
2. Identifying the Components:
- dNdt: This term represents the change in population size over time.
- N: This is the current population density.
- K: This is the carrying capacity, which indicates the maximum population size that the environment can sustain.
3. Focusing on 'r': In the equation, 'r' is a crucial parameter. It is defined as the intrinsic rate of natural increase of the population. This means it reflects how quickly the population can grow under ideal conditions, where resources are unlimited.
4. Understanding 'r' in Context: The value of 'r' is derived from the difference between the birth rate and the death rate in the population. If the birth rate exceeds the death rate, 'r' will be positive, indicating population growth. Conversely, if the death rate exceeds the birth rate, 'r' will be negative, indicating a decline in population.
5. Conclusion: Therefore, 'r' represents the intrinsic rate of natural increase, which is a measure of how fast a population can grow when resources are abundant and environmental conditions are favorable.
- dNdt: This term represents the change in population size over time.
- N: This is the current population density.
- K: This is the carrying capacity, which indicates the maximum population size that the environment can sustain.
Similar Questions
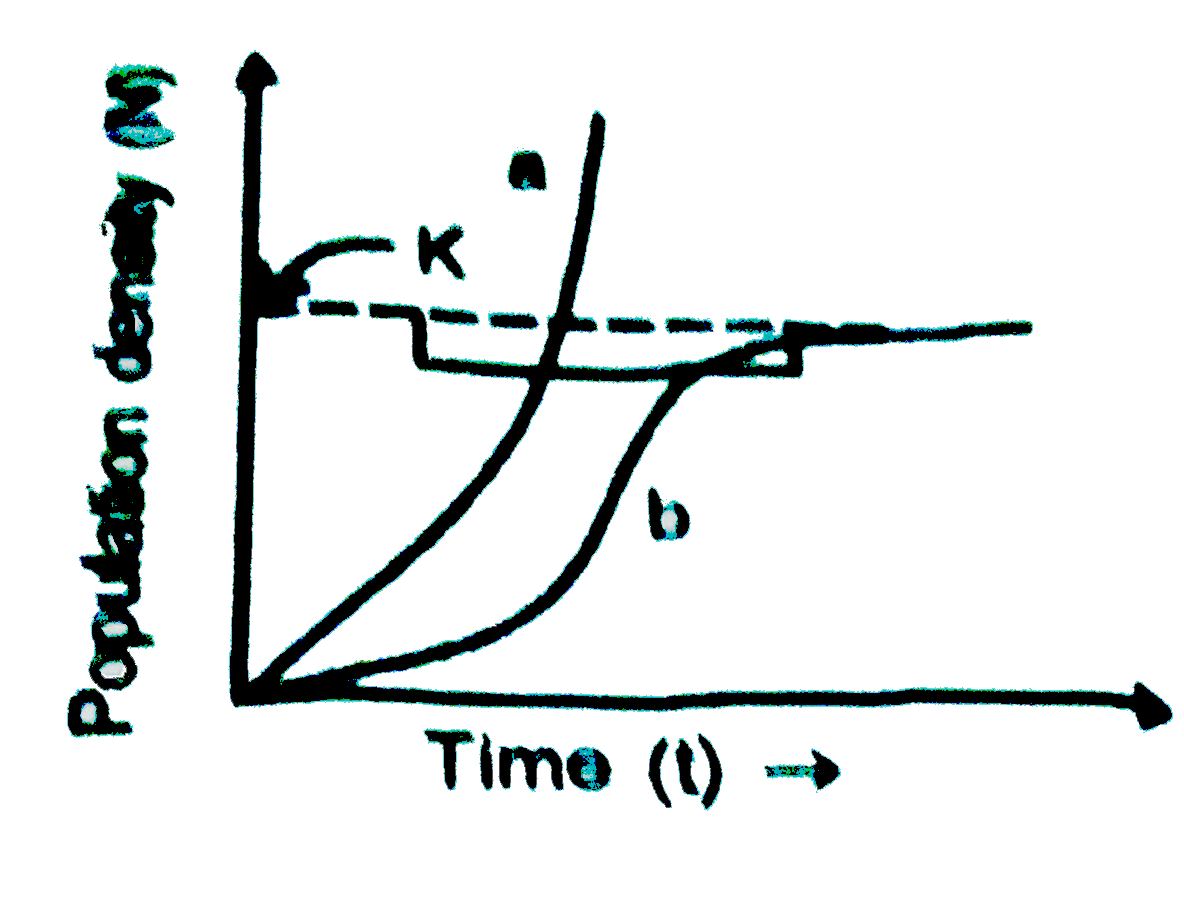
Study the graph given below and answer the questions that follow :
(i) The curve 'b' is described by the following equation :
dNdt=rN{K−NK}
(ii) What does 'K' stand for in this equation ? Mention its significance.
(ii) Which one of the two curves is considered a more realistic one for most of the animal populations ?
(iii) Which curve would depict the population of a species of deer if there are no predators in the habitat ? Why is to so ?
View SolutionIn the equation,dN/dt=rN
View SolutionComplete the following equations :
K+H2O→
View SolutionWhat does 'K' represent in the equation given below?
dNdt=rN(K−NK)
View Solutionwhich of the following option is true for verhulst Pearl logistic growth?
(A)population growth is decreased by the equation dNdt=rN[KK−N].
(B) r' represents biotic potential.
(C) applicable to a population growing in habitat with limited resources.
(D)K represents carrying capacity
View SolutionArithmetic growth curve is represented by which of the following equation?
View SolutionWhat is 'r' in the population equation given : dN/dt = rN
View SolutionCarrying capacity in equation dNdt=rN[K−Nk] is :
View SolutionComplete and balance the following equation : K+O2→
View SolutionFind the general solutions of the following equation: tan3θ=cotθ
View Solution
