which of the following option is true for verhulst Pearl logistic growth?
(A)population growth is decreased by the equation dNdt=rN[KK−N].
(B) r' represents biotic potential.
(C) applicable to a population growing in habitat with limited resources.
(D)K represents carrying capacity
Only (A)
only (B)
A, B and D
B, C and D
The correct Answer is:D
To determine which of the options is true for Verhulst-Pearl logistic growth, let's analyze each option step by step.
Step 1: Understanding the Equation
The logistic growth model is represented by the equation:
dNdt=rN(K−NK)
Where:
- dNdt = rate of change of population size
- r = intrinsic rate of increase (also known as biotic potential)
- K = carrying capacity of the environment
- N = current population size
Step 2: Analyzing Each Option
Option A: "Population growth is decreased by the equation dNdt=rN(K−NK)."
- This statement is misleading. The equation describes how population growth slows down as it approaches the carrying capacity K. It does not imply that growth is decreased by the equation itself; rather, it shows a model of growth that accounts for resource limitations.
Option B: "r represents biotic potential."
- This statement is true. In the logistic growth equation, r indeed represents the intrinsic rate of increase or biotic potential of the population.
Option C: "Applicable to a population growing in habitat with limited resources."
- This statement is also true. The logistic growth model is specifically designed to describe populations that grow in environments where resources are limited, leading to a carrying capacity K.
Option D: "K represents carrying capacity."
- This statement is true. In the logistic growth equation, K is defined as the carrying capacity, which is the maximum population size that the environment can sustain.
Conclusion
Based on the analysis:
- Option A is false.
- Option B is true.
- Option C is true.
- Option D is true.
Thus, the true options for Verhulst-Pearl logistic growth are B, C, and D.
The logistic growth model is represented by the equation:
dNdt=rN(K−NK)
Where:
- dNdt = rate of change of population size
- r = intrinsic rate of increase (also known as biotic potential)
- K = carrying capacity of the environment
- N = current population size
Option A: "Population growth is decreased by the equation dNdt=rN(K−NK)."
- This statement is misleading. The equation describes how population growth slows down as it approaches the carrying capacity K. It does not imply that growth is decreased by the equation itself; rather, it shows a model of growth that accounts for resource limitations.
- This statement is true. In the logistic growth equation, r indeed represents the intrinsic rate of increase or biotic potential of the population.
- This statement is also true. The logistic growth model is specifically designed to describe populations that grow in environments where resources are limited, leading to a carrying capacity K.
- This statement is true. In the logistic growth equation, K is defined as the carrying capacity, which is the maximum population size that the environment can sustain.
Based on the analysis:
- Option A is false.
- Option B is true.
- Option C is true.
- Option D is true.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which of the following equations correctly represents Verhulst-Pearl logistic growth ?
AdN/dt=rN(K−NK)BdN/dt=rNKCdN/dt=N(K−N)KDdN/dt=r(K−N)KThe population growth is generally described by the following equation : dNdt=rN(K−NK) What does 'r' represent in the given equation ?
APopulation density at time 't'BIntrinsic rate of natural increaseCCarrying capacityDThe base of natural logarithm
(i) Which of the following A,B,C ,d represent increases and decreases in population growth ?
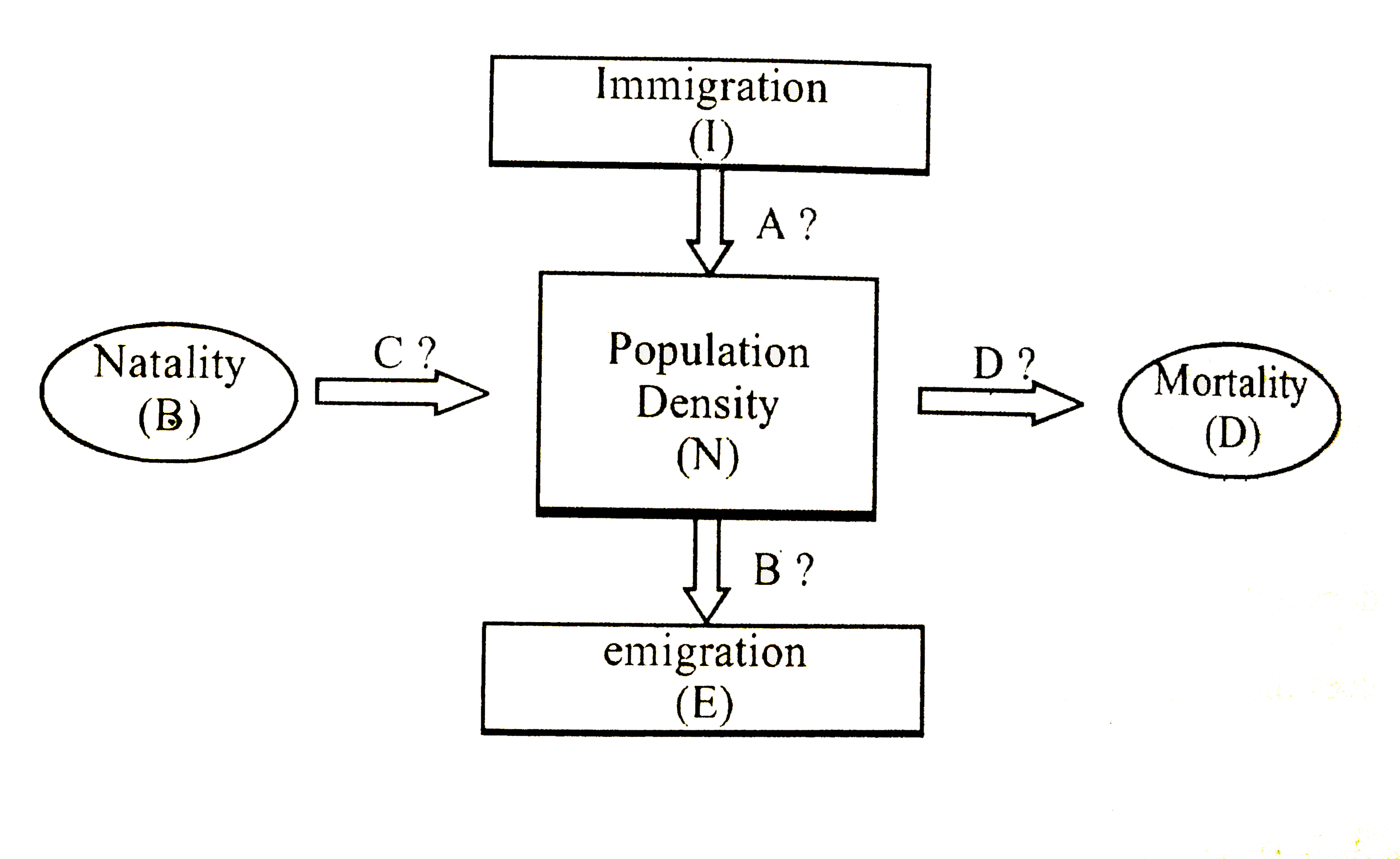
View SolutionCarrying capacity in equation dNdt=rN[K−Nk] is :
View SolutionWhat does 'K' represent in the equation given below?
dNdt=rN(K−NK)
View SolutionWhen does the growth rate of a population following the logistic model equal zero ? The logistic model is given as dN/dt = rN(1-N/K):
View SolutionWhen does the growth rate of a population following the logistic model equal zero ? The logistic model is given as dN/dt = rN(1-N/K):
View SolutionDraw and explain a logistic curve for a population of density (N) at time (t ) whose intrinsic rate of natural increase is (r) and carrying capacity is (k).
View Solution
