What would be the growth rate pattern, when the resources are unlimited?
Exponential or Logistic.
Topper's Solved these Questions
- ORGANISMS AND POPULATIONS BOOK - MODERN PUBLICATIONCHAPTER - ORGANISMS AND POPULATIONS EXERCISE - NCERT FILE NCERT Exemplar Problems (C. SHORT ANSWER TYPE QUESTIONS)
19 Videos
- ORGANISMS AND POPULATIONS BOOK - MODERN PUBLICATIONCHAPTER - ORGANISMS AND POPULATIONS EXERCISE - NCERT FILE NCERT Exemplar Problems (D. LONG ANSWER TYPE QUESTIONS)
12 Videos
- ORGANISMS AND POPULATIONS BOOK - MODERN PUBLICATIONCHAPTER - ORGANISMS AND POPULATIONS EXERCISE - NCERT FILE NCERT Exemplar Problems (A. MULTIPLE CHOICE QUESTIONS)
20 Videos
- MOLECULAR BASIS OF INHERITANCE BOOK - MODERN PUBLICATIONCHAPTER - MOLECULAR BASIS OF INHERITANCE EXERCISE - CHAPTER PRACTICE TEST (Section - E)
1 Videos
- PRINCIPLES OF INHERITANCE AND VARIATIONBOOK - MODERN PUBLICATIONCHAPTER - PRINCIPLES OF INHERITANCE AND VARIATIONEXERCISE - CHAPTER PRACTICE TEST section-e(Long answer type question)
1 Videos
Similar Questions
What do you understand about the growth rate?
View SolutionRead the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
Study the population growth curves (A and B) in the given graph and select the incorrect statement :
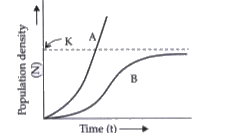
View Solution
Knowledge Check
What was the growth rate according to the 2001 census report?
A1.7%B3.6%C5.2%D0.5%Read the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
Identify the incorrect statement :AExponential growth occurs is organism such as lemmings .BLogistic growth is more relistic .CExponential growth has two phases lag and log .DIn logistic growth, population passes well beyond the carrying capacity of ecosystem.Read the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
The population growth is generally descibed by the following equations :
dN/dt=rN(K−N)/K
What does 'r' represent in the given equation ?APopulation density at time Y.BIntrinsic rate of natural increaseCCarrying capacityDThe base of natural logarithum
Read the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
The equations correctly represents Verhulst-Pearl logistic growth is:
View SolutionRead the following text and answer the following question on the basis of the same :
Growth of population with time shows specific and predictable patters. Two types of growth patter of populaiton are exponetial and logistic growth . When resource in the habitat are unlimited each species has the ability to relize fully its innate potential to grow in number . Then the population gorws in exponential fashion . When the resource are limited growth curve shows an inital slow rate and then it accelerates and finally slows giving the gorwth curve which is sigmoid .
Identify the correct equation that represents the exponential population growth curve:
View SolutionWhat would be the per cent growth or birth rate per individual per hour for the same population mentioned in the previous question ?
View SolutionWhat would be the percent growth or birth rate per individual per hour for the same population mentioned in the previous question (Question 10)?
View SolutionIf feeding efficiency of one species might be reduced due to the interfering and inhibitory presence of the other species, even if resources (food and space) are abundant then it is called
View Solution
