1 mole of each of X1,X2,X3 with van der Waal's constants a (in atm L3mol−2) 1.0, 3.8, 2.1 respectively is kept separately in three different vessels of equal volume at identical temperature. Their pressures are observed to P1,P2, and P3 respectively. On the basis of this data alone, select the correct option (neglect the effect of 'b') :
P1<P2<P3
P2<P1<P3
P2<P3<P1
P1=P2=P3
The correct Answer is:c
To solve the problem, we need to analyze the relationship between the Van der Waals constant a and the pressure exerted by the gases X1,X2, and X3. Here’s a step-by-step solution:
Step 1: Understand the Van der Waals Equation
The Van der Waals equation for real gases is given by:
(P+an2V2)(V−nb)=nRT
Since we are neglecting the effect of b, we can simplify this to:
P+an2V2=nRTV
Where:
- P = pressure of the gas
- a = Van der Waals constant (specific to each gas)
- n = number of moles (1 mole for each gas)
- V = volume of the gas
- R = universal gas constant
- T = temperature
Step 2: Rearranging the Equation
Rearranging the equation gives us:
P=nRTV−an2V2
Since n=1 for each gas, the equation simplifies to:
P=RTV−aV2
Step 3: Analyze the Effect of a
From the equation, we can see that as the value of a increases, the term aV2 becomes larger. This means that the pressure P will decrease because we are subtracting a larger value from the ideal pressure RTV.
Step 4: Compare the Values of a
Given the values of a:
- For X1, a1=1.0
- For X2, a2=3.8
- For X3, a3=2.1
Step 5: Determine the Order of Pressures
Since a2 is the largest, X2 will have the lowest pressure. Next, a3 is larger than a1, so X3 will have a lower pressure than X1. Thus, the order of pressures will be:
P2<P3<P1
This means:
- P2 (for X2) is the lowest,
- P3 (for X3) is in the middle,
- P1 (for X1) is the highest.
Final Answer
The correct order of pressures is:
P2<P3<P1
The Van der Waals equation for real gases is given by:
(P+an2V2)(V−nb)=nRT
Since we are neglecting the effect of b, we can simplify this to:
P+an2V2=nRTV
Where:
- P = pressure of the gas
- a = Van der Waals constant (specific to each gas)
- n = number of moles (1 mole for each gas)
- V = volume of the gas
- R = universal gas constant
- T = temperature
Rearranging the equation gives us:
P=nRTV−an2V2
Since n=1 for each gas, the equation simplifies to:
P=RTV−aV2
From the equation, we can see that as the value of a increases, the term aV2 becomes larger. This means that the pressure P will decrease because we are subtracting a larger value from the ideal pressure RTV.
Given the values of a:
- For X1, a1=1.0
- For X2, a2=3.8
- For X3, a3=2.1
Since a2 is the largest, X2 will have the lowest pressure. Next, a3 is larger than a1, so X3 will have a lower pressure than X1. Thus, the order of pressures will be:
P2<P3<P1
This means:
- P2 (for X2) is the lowest,
- P3 (for X3) is in the middle,
- P1 (for X1) is the highest.
The correct order of pressures is:
P2<P3<P1
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 230videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 14videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Subjective problems14videos
ELECTROCHEMISTRY
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - IONIC EEQUILIBRIUMEXERCISE - Subjective problems1videos
IONIC EEQUILIBRIUM
Similar Questions
The values of the van der Waals constants for a gas a = 4.10 dm6barmol−2 and b = 0.035 dm3mol−1. Calculate the values of the critical temperature and critical pressure for the gas.
View SolutionThe van der Waal's constants a & b of CO2 are 3.64L2mol−2 bar & 0.04Lmol−1 respectively. The value of R is 0.083¯dm3mol−1K−1. If one mole of CO2 is confined to a volume of 0.15Lat300K, then the pressure (in bar) eaxerted by the gas is :
View SolutionCalculate Boyle temperature range for CO2 if its van der Waal's constants a and b are 3.592 atm litre2 mole2andb=0.0427 litre mole−1.
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionGiven p A.P's , each of which consists on n terms . If their first terms are 1,2,3…… p and common differences are 1,3,5,……,2p−1 respectively , then sum of the terms of all the progressions is
View SolutionThree containes of the same volume contain three different gases. The masses of the molecules are m1,m2 and m3 and the number of molecules in their respective containers are N1,N2 and N3. The gas pressure in the containers are P1,P2 and P3 respectively. All the gases are now mixed and put in one of the containers. The pressure P of mixture will be
View SolutionTwo solutions of KNO3 and CH3COOH are prepared separately. The molarity of both is 0.1M and osmotic pressure is P1 and P2, respectively.
The correct relationship between the osmotic pressure isView SolutionIf P1,P2 and P3 are the altitudes of a triangle from vertices A,B and C respectively and Δ is the area of the triangle, then the value of 1P1+1P2−1P3=
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
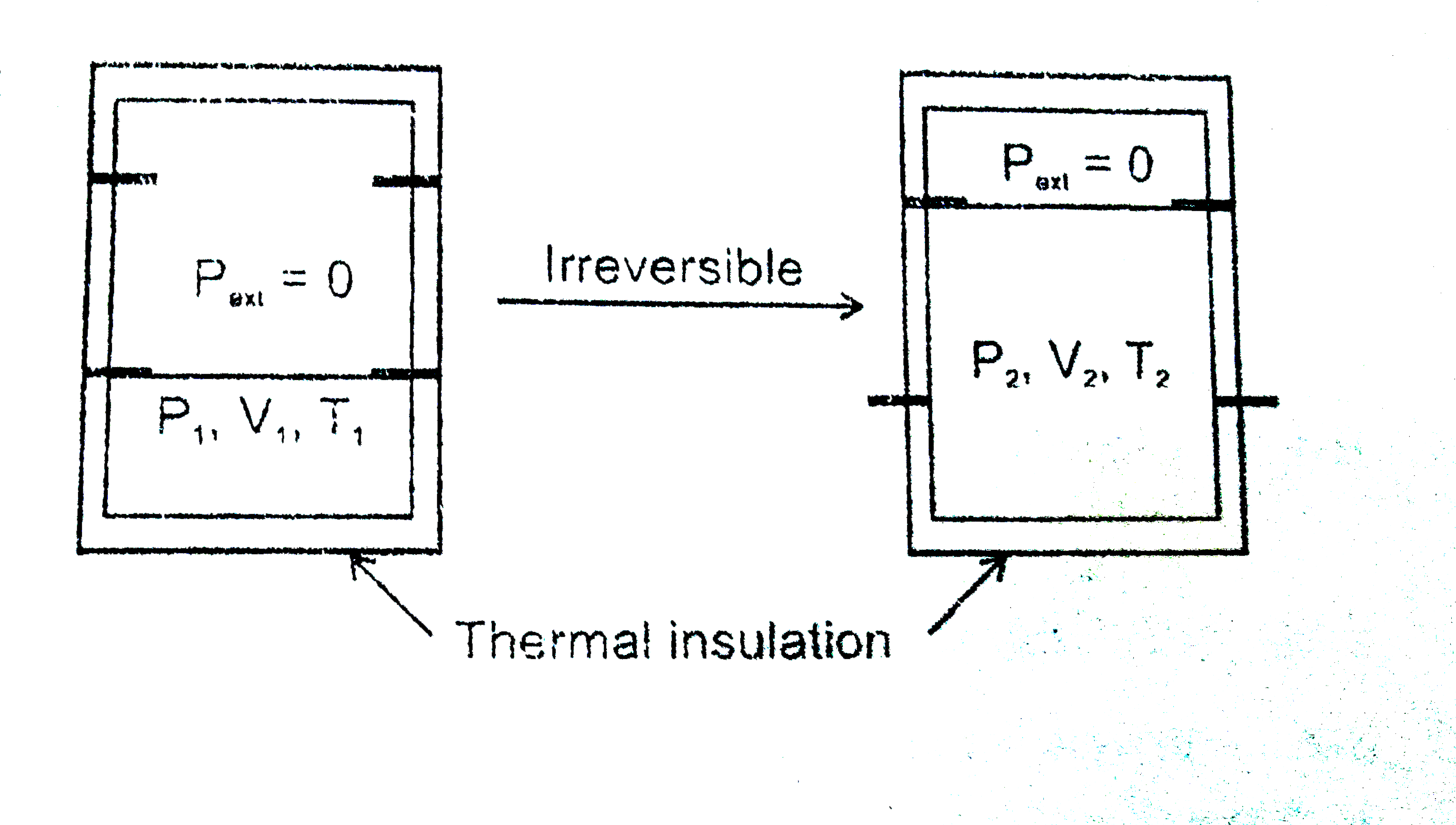 View Solution
View Solution
