A balloon contains 14.0 L of air at 760 torr. What will be the volume of the balloon when it is taken to a depth of 10 ft. in a swimming pool? Assume that the temperature of the air and water are equal. (density : Hg=13.6g/mL.)
11
11.3
10
10.8
The correct Answer is:d
To find the volume of the balloon at a depth of 10 feet in a swimming pool, we can use the principles of gas laws, specifically Boyle's Law, which states that for a given mass of gas at constant temperature, the product of pressure and volume is constant (P1V1 = P2V2).
Step 1: Identify the initial conditions.
- Initial volume (V1) = 14.0 L
- Initial pressure (P1) = 760 torr
Step 2: Convert the initial pressure to Pascals.
- 1 torr = 133.322 Pa
- P1 = 760 torr × 133.322 Pa/torr = 101325 Pa
Step 3: Calculate the pressure at a depth of 10 feet.
- First, convert feet to meters:
- 10 ft = 10 × 0.3048 m = 3.048 m
- Calculate the pressure increase due to the water column:
- Pressure increase (hρg) = height × density of water × gravitational acceleration
- Density of water = 1000 kg/m³
- Gravitational acceleration (g) = 9.81 m/s²
- hρg = 3.048 m × 1000 kg/m³ × 9.81 m/s² = 29953.88 Pa
- Total pressure at depth (P2) = atmospheric pressure + pressure due to water
- P2 = 101325 Pa + 29953.88 Pa = 131278.88 Pa
Step 4: Use Boyle's Law to find the final volume (V2).
- According to Boyle's Law: P1V1 = P2V2
- Rearranging gives us: V2 = (P1V1) / P2
- Substitute the values:
- V2 = (101325 Pa × 14.0 L) / 131278.88 Pa
- V2 = 10.8 L (approximately)
Final Answer:
The volume of the balloon when taken to a depth of 10 feet in a swimming pool is approximately 10.8 liters.
---
- Initial volume (V1) = 14.0 L
- Initial pressure (P1) = 760 torr
- 1 torr = 133.322 Pa
- P1 = 760 torr × 133.322 Pa/torr = 101325 Pa
- First, convert feet to meters:
- 10 ft = 10 × 0.3048 m = 3.048 m
- Calculate the pressure increase due to the water column:
- Pressure increase (hρg) = height × density of water × gravitational acceleration
- Density of water = 1000 kg/m³
- Gravitational acceleration (g) = 9.81 m/s²
- hρg = 3.048 m × 1000 kg/m³ × 9.81 m/s² = 29953.88 Pa
- Total pressure at depth (P2) = atmospheric pressure + pressure due to water
- P2 = 101325 Pa + 29953.88 Pa = 131278.88 Pa
- According to Boyle's Law: P1V1 = P2V2
- Rearranging gives us: V2 = (P1V1) / P2
- Substitute the values:
- V2 = (101325 Pa × 14.0 L) / 131278.88 Pa
- V2 = 10.8 L (approximately)
The volume of the balloon when taken to a depth of 10 feet in a swimming pool is approximately 10.8 liters.
Topper's Solved these Questions
- GASEOUS STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 2
30 Videos
- GASEOUS STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 1
4 Videos
- ELECTROCHEMISTRYBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Subjective problems
14 Videos
- IONIC EEQUILIBRIUMBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - IONIC EEQUILIBRIUMEXERCISE - Subjective problems
1 Videos
Similar Questions
A partially inflated balloon contains 500m3 of helium at 27∘C and 1atm pressure. What is the volume of the helium at an altitude of 18000ft, where the pressure is 0.5atm and the temperature is −3∘C ?
View SolutionA weather balloon has a volume of 175 L when filled with hydrogen at a pressure of 1.000 atm. Calculate the volume of the balloon when it rises to a height of 2000 m, where atmospheric pressure is 0.8000 atm. Assume that temperature is constant.
View SolutionOn a ship sailing in pacific ocean where temperature is 23.4∘C, a balloon is filled with 2L air. What will be the volume of the balloon when the ship reaches Indian ocean, Where temperature is 26.1∘C?
View SolutionA high-altitude balloon is filled with 1.41×104L of hydrogen at a temperature of 21∘C and a pressure of 745 torr. What is the volume of the balloon at a height of 20 km, where the temperature is −48∘C and the pressure is 63.1 torr?
View SolutionAn open container has dimensions of 4.0m×5.0m and height of 3.0 m.
(i) Find the weight of the air in the container at 20∘C.
(ii) What is the weight of an equal volume of water ? Also find pressure at the base of container due to this weight pof water.
(iii) What is the total downward force on the base of the container due to air pressure of 1.0 atm ?
Take the denities of air and water as 1.2kg/m3 and 103kg/m3 respectively.
View SolutionA spherical balloon contains air at temperature T0 and pressure P0. The balloon material is such that the instantaneous pressure inside is proportional to the square of the diameter. When the volume of the balloon doubles as a result of heat transfer, the expansion follows the law
View SolutionA piece of gold weighs 10g in air and 9g in water. What is the volume of cavity? (Density of gold =19.3gcm−3)
View SolutionA manometer contains a liquid of density 5.44g/cm3 is attached to a flask containing gas 'A' as follows
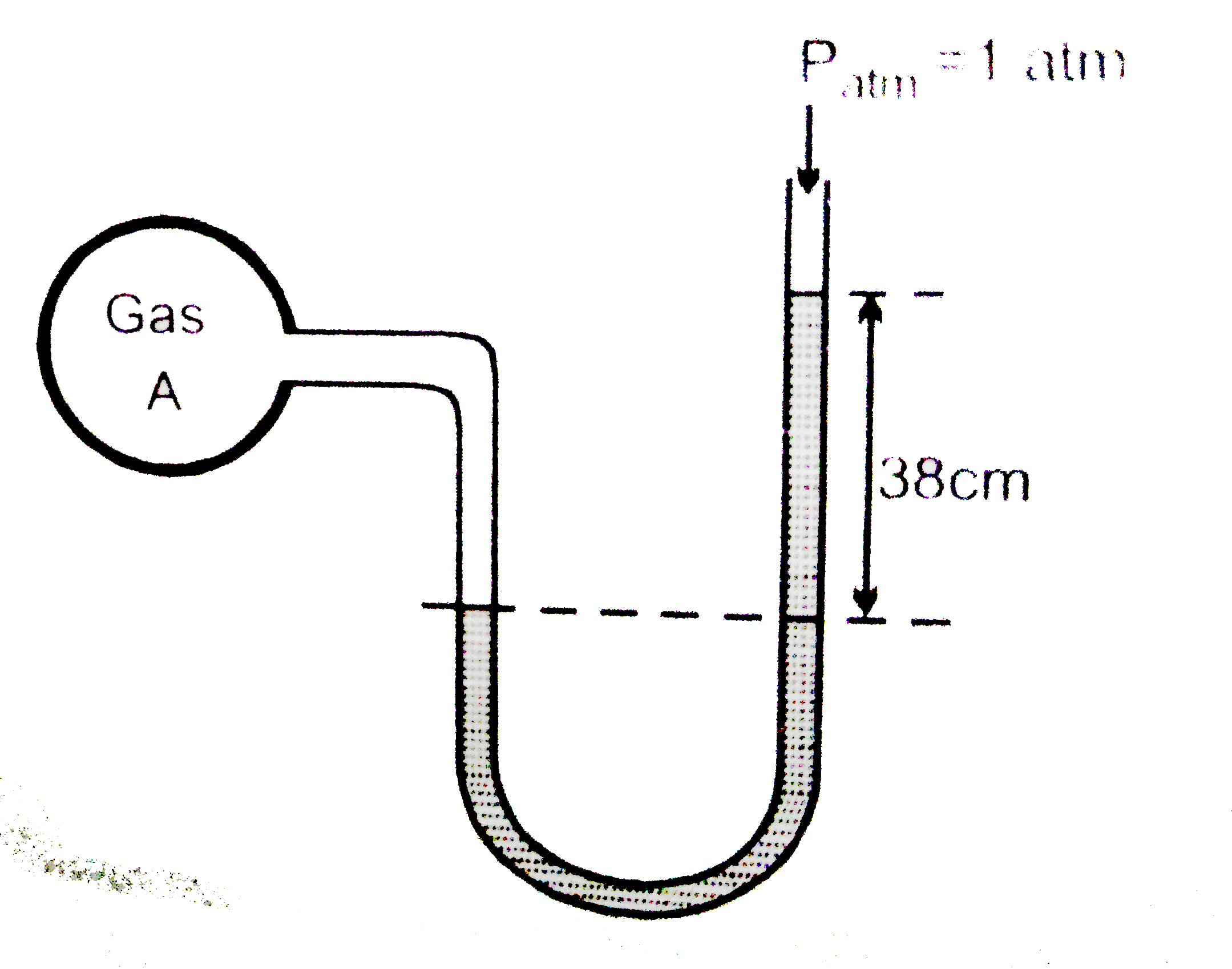
If the same liquid is used in barometer to measure the atmospheric pressure, then what will be the lengh of the liquid columnm which exerts pressure equal to 1 atm ? (density of Hg=13.6g/cm3)
View SolutionA capillary due sealed at the top has an internal radius of r=0.05cm. The tube is placed vertically in water, with its open end dipped in water. Find greatest interger corresponding to the length (in water) of such a tube be for the water in it to rise in these conditions to a height h=1cm ? The pressure The pressure of the air is P0=1atm. =7cm of Hg , density of Hg=13.6/cm3, g=9.8m/sec2 The surface tension of water is σ=70dyne/cm. (assume temperature of air in the tube is constant)
View SolutionA monometer contains a liquid of density 5.44g/cm3 is attached to a flask containing gas A'asfollows<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NRA_PHY_CHM_JMA_C03_E01_213_Q01.pngwh=80%sty≤=background:white;><br>Ifthesameliqusused∈¯ometer→measuretheatmosphericpressure,thenwˆwillbethe≤n>hoftheliquolumn,whichexertspressureequal→1atm?(densityofHg=13.6g//cm^(3))
View Solution
