A spherical balloon contains air at temperature T0 and pressure P0. The balloon material is such that the instantaneous pressure inside is proportional to the square of the diameter. When the volume of the balloon doubles as a result of heat transfer, the expansion follows the law
PV= constant
PV2/5= constant
PV−1= constant
PV−2/3= constant
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the pressure, volume, and diameter of the balloon as it expands. Here's a step-by-step solution:
Step 1: Understand the relationship between pressure and diameter
We are given that the pressure inside the balloon (P) is proportional to the square of the diameter (d). This can be expressed mathematically as:
P∝d2
or
P=k⋅d2
where k is a constant of proportionality.
Step 2: Relate volume and diameter
For a spherical balloon, the volume (V) is given by the formula:
V=43π(d2)3=πd36
Thus, we can express the diameter in terms of volume:
d=(6Vπ)1/3
Step 3: Analyze the change in volume
We know that the volume of the balloon doubles as a result of heat transfer:
V2=2V1
This means:
V2V1=2
Step 4: Relate the diameters before and after expansion
Using the relationship between volume and diameter, we can write:
d2d1=(V2V1)1/3=21/3
Step 5: Relate the pressures before and after expansion
Using the relationship between pressure and diameter, we can express the pressures before and after the expansion:
P2P1=(d2d1)2=(21/3)2=22/3
Step 6: Combine the relationships
From the relationships derived, we can express the pressures and volumes in a combined form:
P2⋅V−232=P1⋅V−231
This indicates that the product of pressure and volume raised to the power of −23 remains constant during the expansion.
Conclusion
Thus, we conclude that during this expansion process, the relationship follows:
PV−23=constant
We are given that the pressure inside the balloon (P) is proportional to the square of the diameter (d). This can be expressed mathematically as:
P∝d2
or
P=k⋅d2
where k is a constant of proportionality.
For a spherical balloon, the volume (V) is given by the formula:
V=43π(d2)3=πd36
Thus, we can express the diameter in terms of volume:
d=(6Vπ)1/3
We know that the volume of the balloon doubles as a result of heat transfer:
V2=2V1
This means:
V2V1=2
Using the relationship between volume and diameter, we can write:
d2d1=(V2V1)1/3=21/3
Using the relationship between pressure and diameter, we can express the pressures before and after the expansion:
P2P1=(d2d1)2=(21/3)2=22/3
From the relationships derived, we can express the pressures and volumes in a combined form:
P2⋅V−232=P1⋅V−231
This indicates that the product of pressure and volume raised to the power of −23 remains constant during the expansion.
Thus, we conclude that during this expansion process, the relationship follows:
PV−23=constant
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects
29 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective
22 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
A spherical balloon contains 1 mole of He at T0. The balloon material is such that the pressure inside is alwaus proportional to square of diameter. When volume of balloon becomes 8 times of initial volume, then :-
View SolutionA balloon containing 1 mole air at 1 atm initially is filled further with air till pressure increases to 4 atm. The intial diameter of the ballon is 1 m and the pressure at each stage is proportional to diameter of the balloon. How many moles of air added to change the pressure from 1 atm to 4 atm.
View Solution
Knowledge Check
A gas is filled in a container at pressure P0. If the mass of molecules is halved and their rms speed is doubled, then the resultant pressure would be
A2P0B4P0CP04DP02
A gas is filled in a container at pressure P0. If the mass of molecules is halved and their rms speed is doubled, then the resultant pressure would be
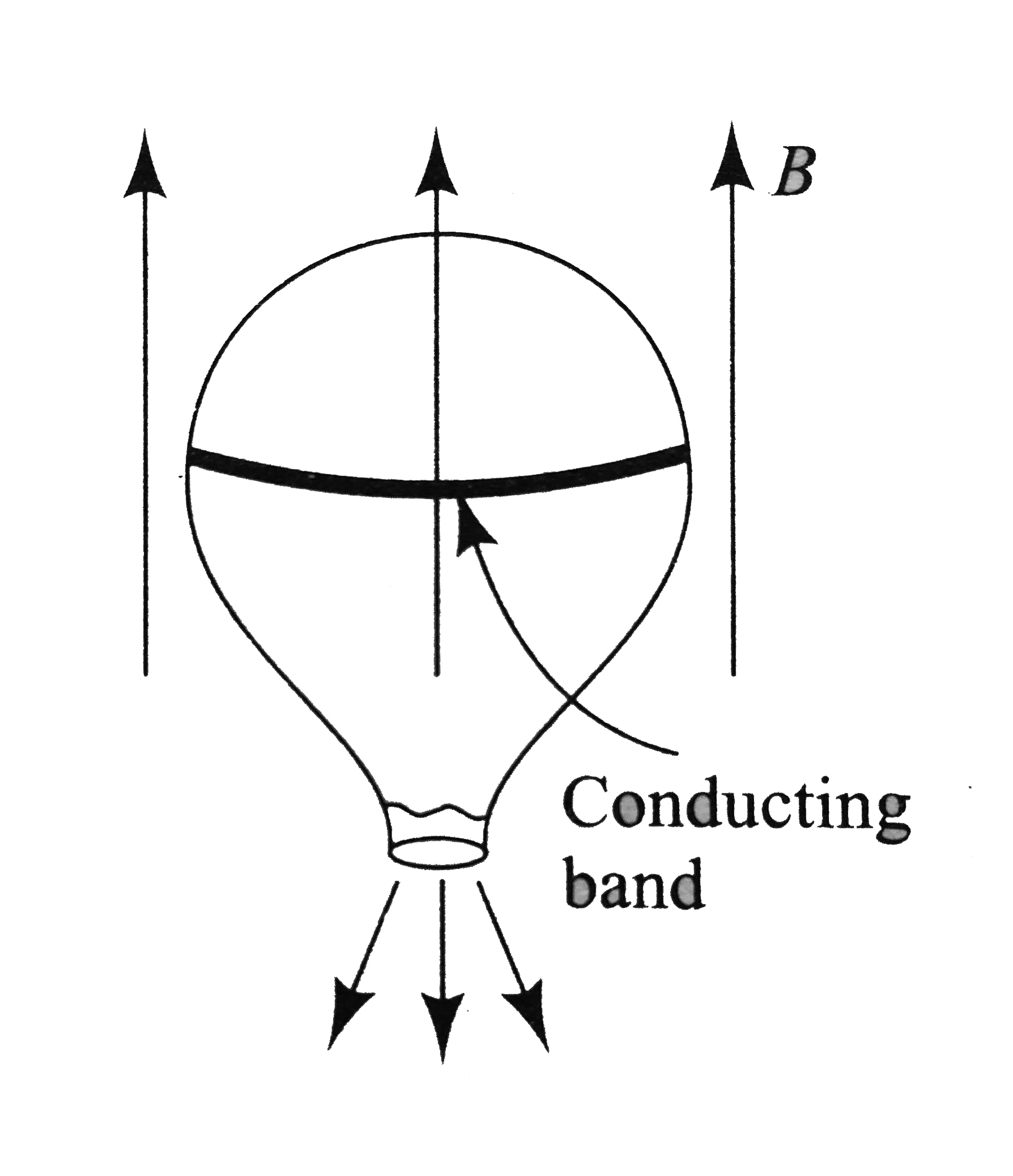
View SolutionAn elasticized conducting band is around a spherical ballon . Its plane through the center of the balloon. A uniform nmagnetic field of magnitude 0.04T is directed perpendicular to the plane of the band. Air is let out of the balloon at 100cm3s−1 at an instant when the radius of the balloon is 10cm. The induced emf in the band is
View SolutionGas at a pressure P0 in contained as a vessel. If the masses of all the molecules are halved and their speeds are doubles. The resulting pressure P will be equal to
View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View SolutionTwo balloons are filled one with pure He gas and the other with air respectively. If the pressure and temperature of these balloons are same, then the number of molecules per unit volume is
View SolutionRadius of a spherical balloon is increasing with respect to time at the rate of 2/π m/s. Find the rate of change in volume (in m3/s) of the balloon when radius is 0.5 m?
View SolutionA balloon contains 14.0 L of air at 760 torr. What will be the volume of the balloon when it is taken to a depth of 10 ft. in a swimming pool? Assume that the temperature of the air and water are equal. (density : Hg=13.6g/mL.)
View Solution