A cinema hall has equidistant rows 1m apart. The length of the cinema hall is 287m and it has 287 rows. From one side of the cinema hall, laughing gas (N2O) is released and from the other side, weeping gas (C6H5COCH2Cl) is released. In which rows, spectors will be laughing and weeping simultaneously?

Molar weight of C8H7Ocl=8×12+7×1+16+35.5
=154.5g.
Molar weight of N2O=2×14+16=44g
According to Graham's law of diffusion,
rN2OrC8H7OCl=√MC8H7OClMN2O=√154.544=√3.5=1.87:1
dN2O=1.872.87×287=187th row from N2O side
dC8H7OCl=1.02.87×287=100th row from weeping gas side.
Therefore, the spectator from the side of N2O in the 187throw will be laughing and weeping simultaneously. Alternatively, the spectator from the side of weeping gas in the 100th row will be laughing and weeping simultaneously.
Topper's Solved these Questions
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Illustration
2 Videos
- STATES OF MATTERBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STATES OF MATTEREXERCISE - Exercises
21 Videos
- SOME BASIC CONCEPTS AND MOLE CONCEPTBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOME BASIC CONCEPTS AND MOLE CONCEPTEXERCISE - Archives Subjective
11 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
A classroom consists 10 equidistant bench. If nitrous oxide (laughing gas) is released from the first desk and tear gas (C6H11Obr) is released from last desk. Find out the desk from 1st at which students starts laughing and weeping simultaneously.
View SolutionA teacher enters a classroom from front door while a student from back door. There are 13 equidistant rows of benches in the classroom. The teacher releases N2O, the laughing gas, from the first bench while the student releases the weeping gas (C6H11OBr) from the last bench. At which row will the students starts laughing and weeping simultaneously?
View SolutionA block of mass M slides along the sides of bowl as shown in the figure. The walls of the bowl are frictionless and the base has coefficient of friction 0.1, and length 0.5m. The block is released from the point A which is 0.2 m high as shown in figure. Then the block comes to rest
View Solutionone end of a spring of natural length ha and spring constant k is fixed at the ground and the other is fitted with a smooth ring of mass m which is allowed to slide on a horizontal rod fixed at a height h figure. Initially, the spring makes an angle of 370 with the vertical when the system is released from rest. find the speed of the ring when the spring becomes vertical.

View SolutionA vertical lamp-post, 6m high, stands at a distance of 2 m from a wall, 4 m high . A 1.5 m tall man starts to walk away from the wall on the other side of the wall, in line with the lamp-post the maximum distance to which the man can walk remaining in the shadow is
View SolutionA current i, indicated by the crosses in figure, is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angle to the strip.
(a) Calculate the drift velocity vd of the electrons.
(b) What are the magnitude and direction of the magnetic force F acting on the electrons?
(c) What should the magnitude and direction of a homogeneous electric field E be in order to counterbalance the effect of mangetic field?
(d) Calculate voltage V necessary between two sides of the conductor in order to creat this field E Between which sides of the conductor would this voltage have to be applied?
(e) If no electric field is applied from the outside, the electrons will be pushed somewhat to one side and therefore will give rise to a uniform electric field EH across the conductor until the forces of this electrostatic field EH balance the magnetic forces encountered in part (b). What will be the magnitude and direction of field EH?
Assume that n, the number of conductor electrons per unit volume is 1.1×1029m−3,h=0.02m,w=0.1cm,i=50A,andB=2T.

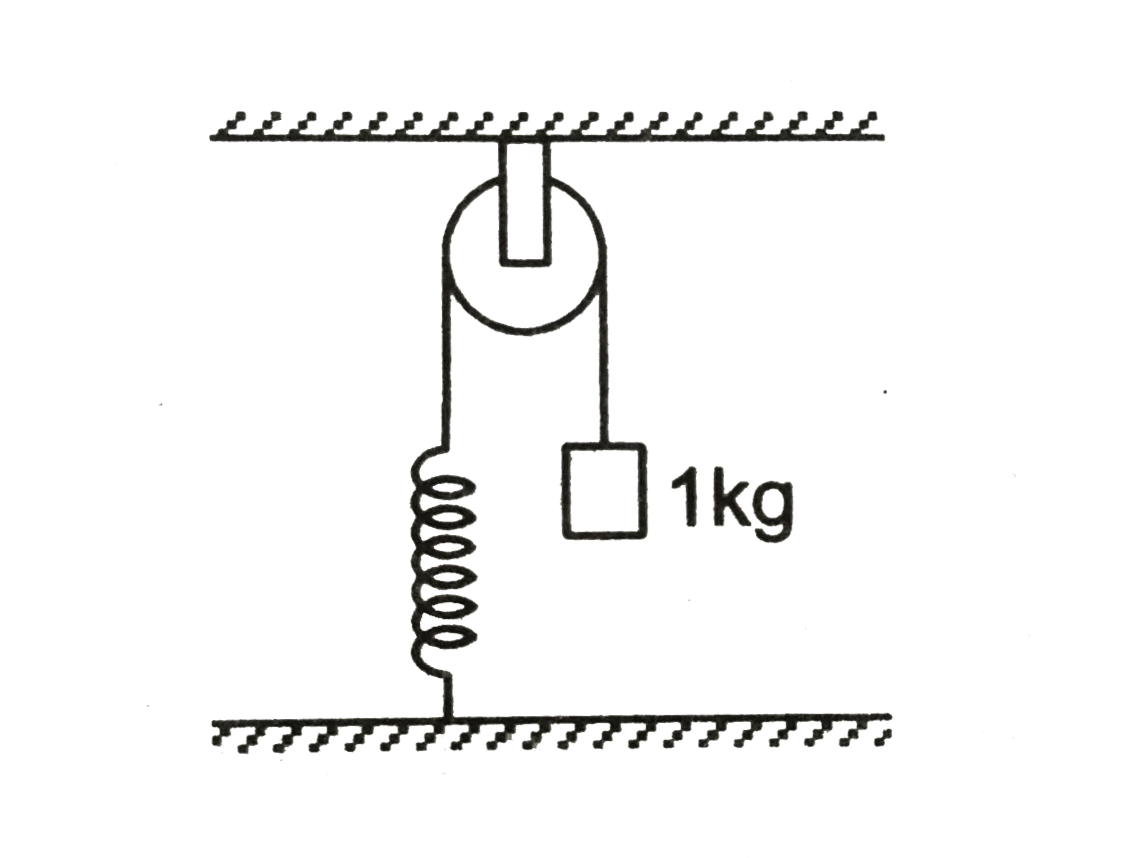
View SolutionThe pulley shown in figure has a radius of 20 cm and moment of inertial 0.2 kg-m^2. The string going over it is attached at one end to a vertical sprign of spring constant 50 N/m fixed from below and supports a 1 kg mas at other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has desceds through 10 cm. Take g=10ms2.
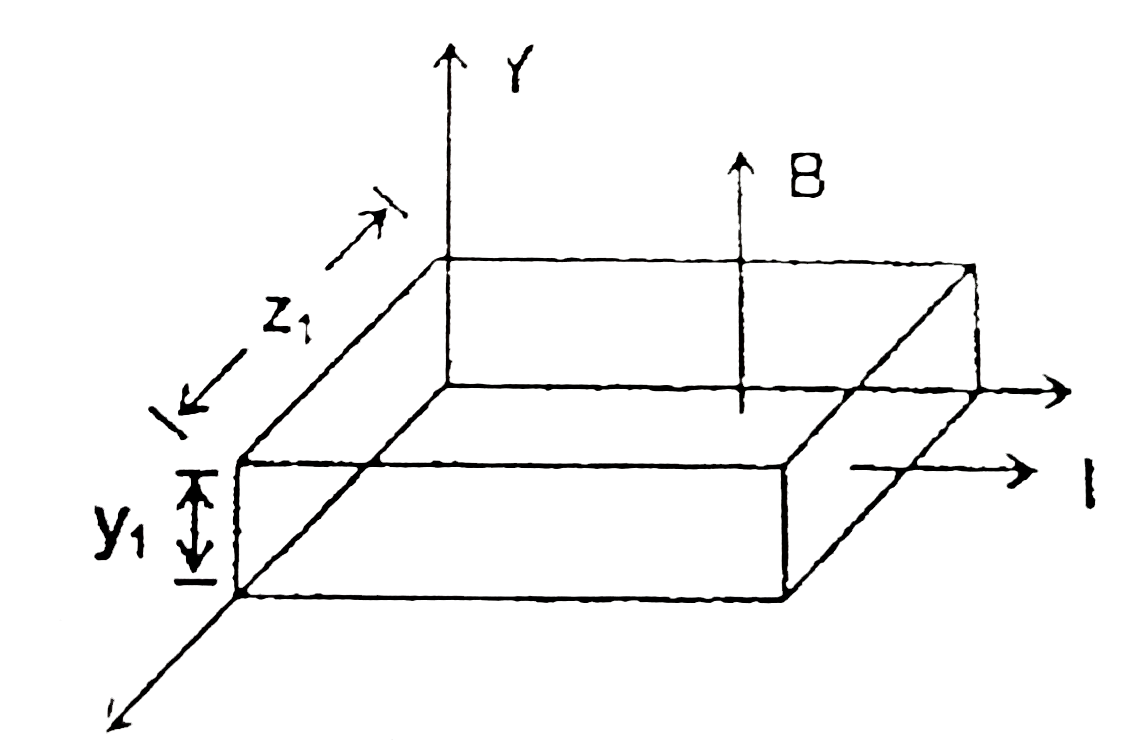
View SolutionThe basic principle underlying the Hall effect is the Lorentz force. When an electron moves along a direction perpendicular to an applied magnetic field, it experiences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an n-type, bar-shaped semiconductor, the carriers are predominantly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward y-axis. Electrons subjected to the lorentz force initially drift away from the current line toward the negative z-axis, resulting in an excess surface electrical charge on the sides of the sample. This charge results in the hall voltage, a potential drop across the two sides of the sample.
The transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnd, where I is the current, B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure. (z1=11.8mm and y1=0.23mm) carrying a current of 120A in the x-direction in a uniform magnetic field B=0.95T. If electron density is 5.85×1028/m3, then
What is the value of hall emf ?
View SolutionThe string is now replaced by a spring of spring constant k and natural length l. Mass 2m is fixed at the bottom of the frame . The mass m which has the other end of the spring attached to it is brought near the mass 2m and released as shown in figure. The maximum angle θ that the spring will substend at the centre will be :( Take k=10N/m,l=1m,m=1kg and l=r)

View SolutionThe space between two large horizontal metal plates, 6cm apart, is filled with a liquid of viscosity 0.8N/m2 . A thin plate of surface area 0.01m2 is moved parallel to the length of the plate such that the plate is at a distance of 2m from one of the plates and 4cm from the other. If the plate moves with a constant speed of 1ms−1, then
View Solution
