A plot of log (a-x) against time 't' is a straight line. This indicates that the reaction is of :
zero order
first order
second order
third order
The correct Answer is:B
To determine the order of the reaction based on the plot of log(a - x) against time 't', we can follow these steps:
1. Understand the Variables:
- Let 'a' be the initial concentration of the reactant.
- Let 'x' be the amount of reactant that has reacted at time 't'.
- Therefore, (a - x) is the concentration of the reactant remaining at time 't'.
2. Identify the Reaction Order:
- For a zero-order reaction, the rate of reaction is constant and does not depend on the concentration of the reactant. The integrated rate law is:
(A)=(A0)−kt
where (A) is the concentration at time t, (A_0) is the initial concentration, and k is the rate constant. The plot of (A) vs. time would yield a straight line, but not log((A)) vs. time.
- For a first-order reaction, the integrated rate law is:
ln(A)=ln(A0)−kt
or rearranging gives:
log(a−x)=loga−k2.303t
This equation indicates that a plot of log(a - x) against time 't' will yield a straight line with a negative slope, confirming it is a first-order reaction.
- For a second-order reaction, the integrated rate law is:
1(A)=1(A0)+kt
This does not involve logarithmic terms, hence a plot of log(a - x) against time would not yield a straight line.
3. Conclusion:
- Since the plot of log(a - x) against time 't' is a straight line, we conclude that the reaction is of first order.
Final Answer:
The reaction is of first order.
- Let 'a' be the initial concentration of the reactant.
- Let 'x' be the amount of reactant that has reacted at time 't'.
- Therefore, (a - x) is the concentration of the reactant remaining at time 't'.
- For a zero-order reaction, the rate of reaction is constant and does not depend on the concentration of the reactant. The integrated rate law is:
(A)=(A0)−kt
where (A) is the concentration at time t, (A_0) is the initial concentration, and k is the rate constant. The plot of (A) vs. time would yield a straight line, but not log((A)) vs. time.
ln(A)=ln(A0)−kt
or rearranging gives:
log(a−x)=loga−k2.303t
This equation indicates that a plot of log(a - x) against time 't' will yield a straight line with a negative slope, confirming it is a first-order reaction.
1(A)=1(A0)+kt
This does not involve logarithmic terms, hence a plot of log(a - x) against time would not yield a straight line.
- Since the plot of log(a - x) against time 't' is a straight line, we conclude that the reaction is of first order.
The reaction is of first order.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - OP TANDONCHAPTER - CHEMICAL KINETICSEXERCISE - OBJECTIVE QUESTIONS (LEVEL-B) SET I
48 Videos
- CHEMICAL KINETICSBOOK - OP TANDONCHAPTER - CHEMICAL KINETICSEXERCISE - OBJECTIVE QUESTIONS (LEVEL-B) SET II
13 Videos
- CHEMICAL KINETICSBOOK - OP TANDONCHAPTER - CHEMICAL KINETICSEXERCISE - PRACTICE PROBLEMS
70 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - OP TANDONCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Integer
4 Videos
- Chemical Thermodynamics and ThermochemistryBOOK - OP TANDONCHAPTER - Chemical Thermodynamics and ThermochemistryEXERCISE - Self Assessment (Integer type).
3 Videos
Similar Questions
Knowledge Check
For the order reaction , plot of log10(a−x) against time t is a straight line with a negative slope equal to ________.
A−2.303KB−2.303kCk2.303D2.303kFor the first order reaction , plot of log10(a−x) against tine 't' is a straight line with slope equal to __________.
A−2.303KB−2.303KC)−k2.303D2.303)KA graph between time (t) and the substance consumed at any time is found to be a straight line passing through the orginal This indicates that the reaction is of :
Azero orderBfirst orderCSecond orderDfractional order
In accordance to Arrhenius equation, the plot of log k against 1T is a straight line. The slope of the line is equal to
View SolutionIf a plant of log10 C versust t gives a straight line for a given reaction, then the reaction is :
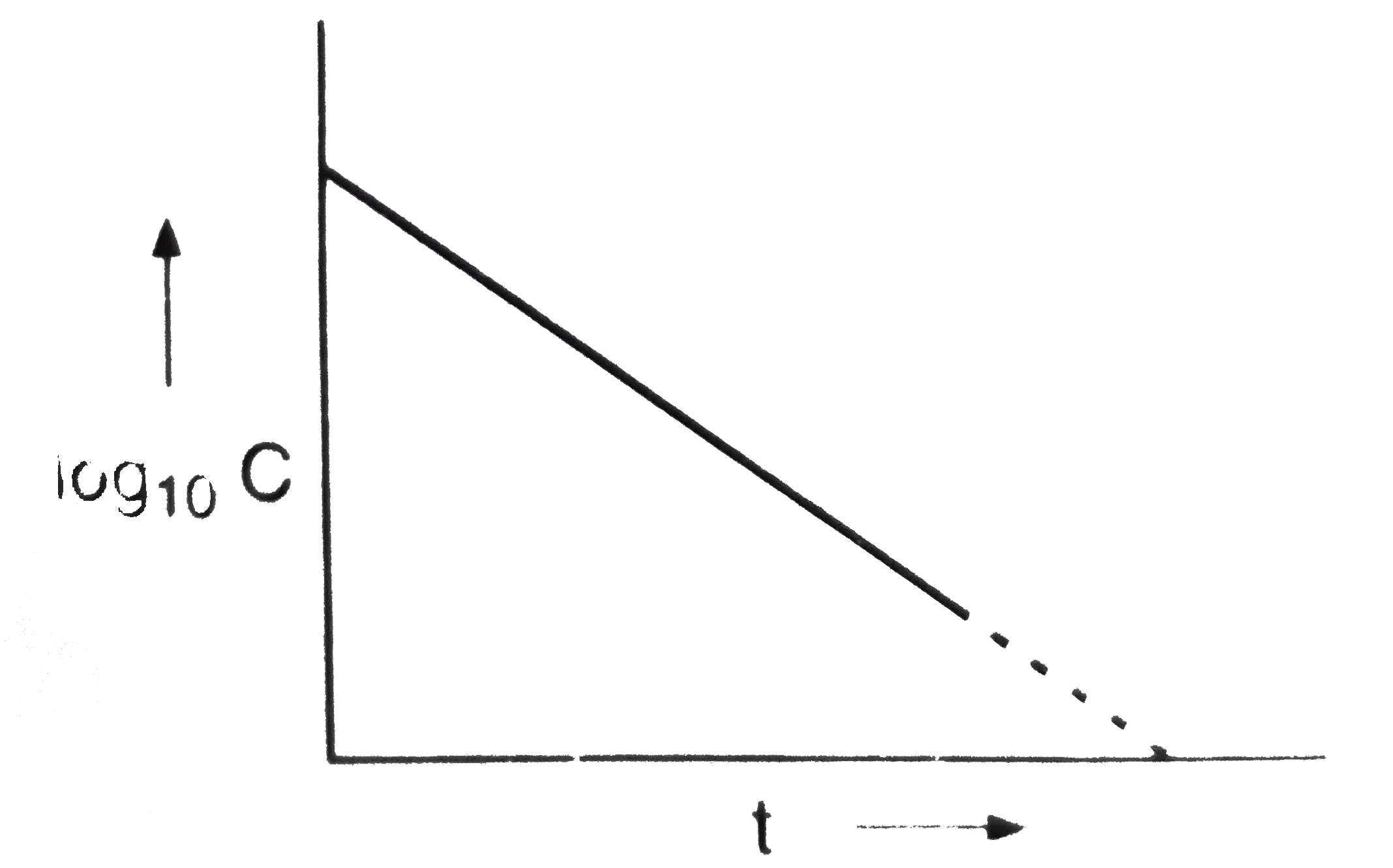
View SolutionFor a certain reaction, a plot of [C0−C]C against time t, yields a straight line. C0 and C are concentrations of reaction at t=0 and t=t respectively. The order of reaction is:
View SolutionFor a given reaction the logarithm of the concentration of the reactant plotted against time gave a straight line with negative slope . The order of the reaction is
View SolutionIn the reaction A+B→C+D, the rate (dxdt) when plotted against time 't' gives a straight line parallel to time aixs.
The order and rate of reaction will be:
View Solution
