Among the following curves, which is not according to Charle's law ?
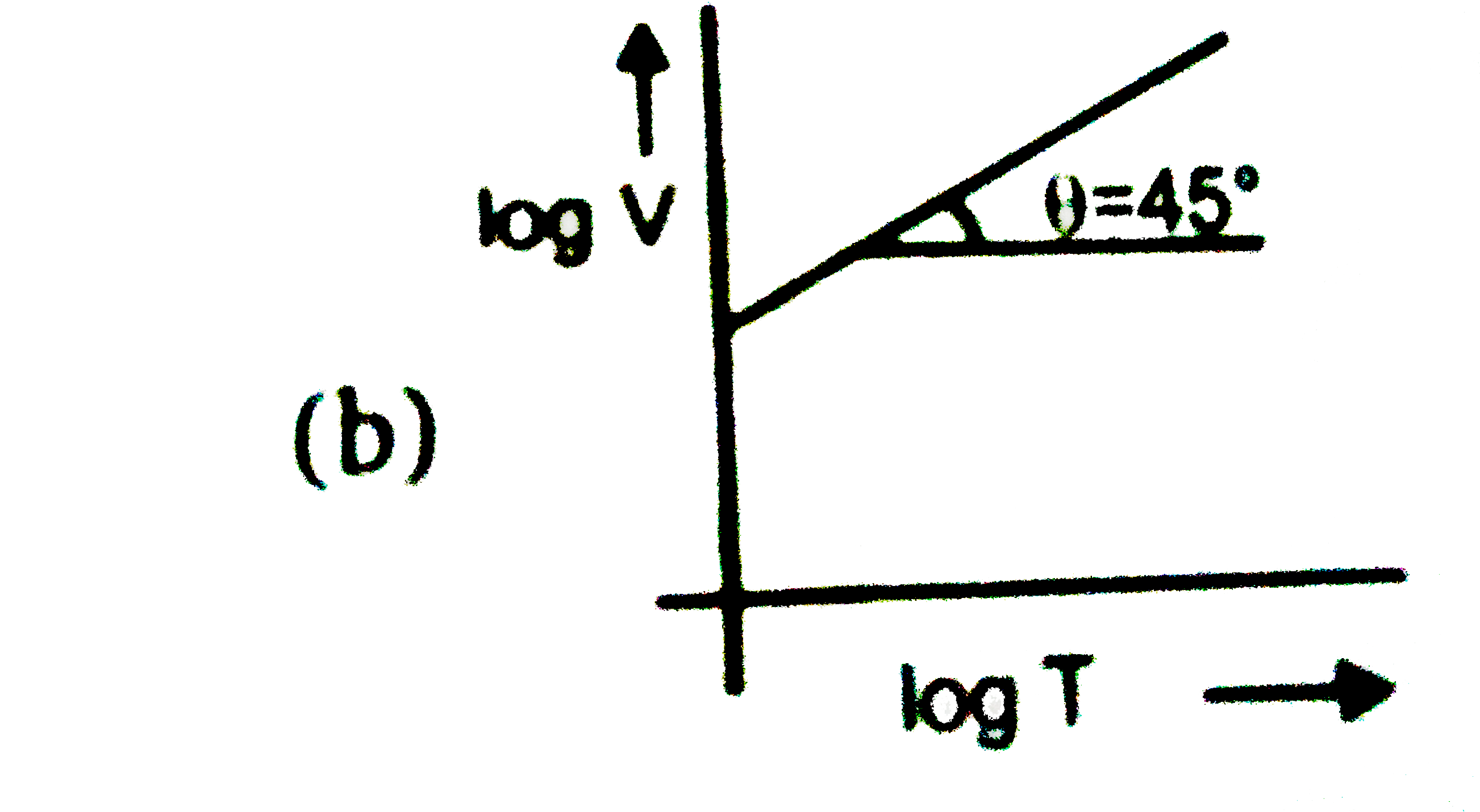
The correct Answer is:d
To determine which of the given curves is not according to Charles's law, we need to first understand what Charles's law states.
1. Understanding Charles's Law:
- Charles's law states that for a fixed amount of gas at constant pressure, the volume (V) of the gas is directly proportional to its absolute temperature (T). This can be mathematically expressed as:
V∝T(at constant pressure)
- This can also be written as:
V=kT
where k is a constant.
2. Identifying the Graphs:
- We need to analyze the given options (curves) to see which one does not represent the relationship described by Charles's law.
3. Analyzing Each Option:
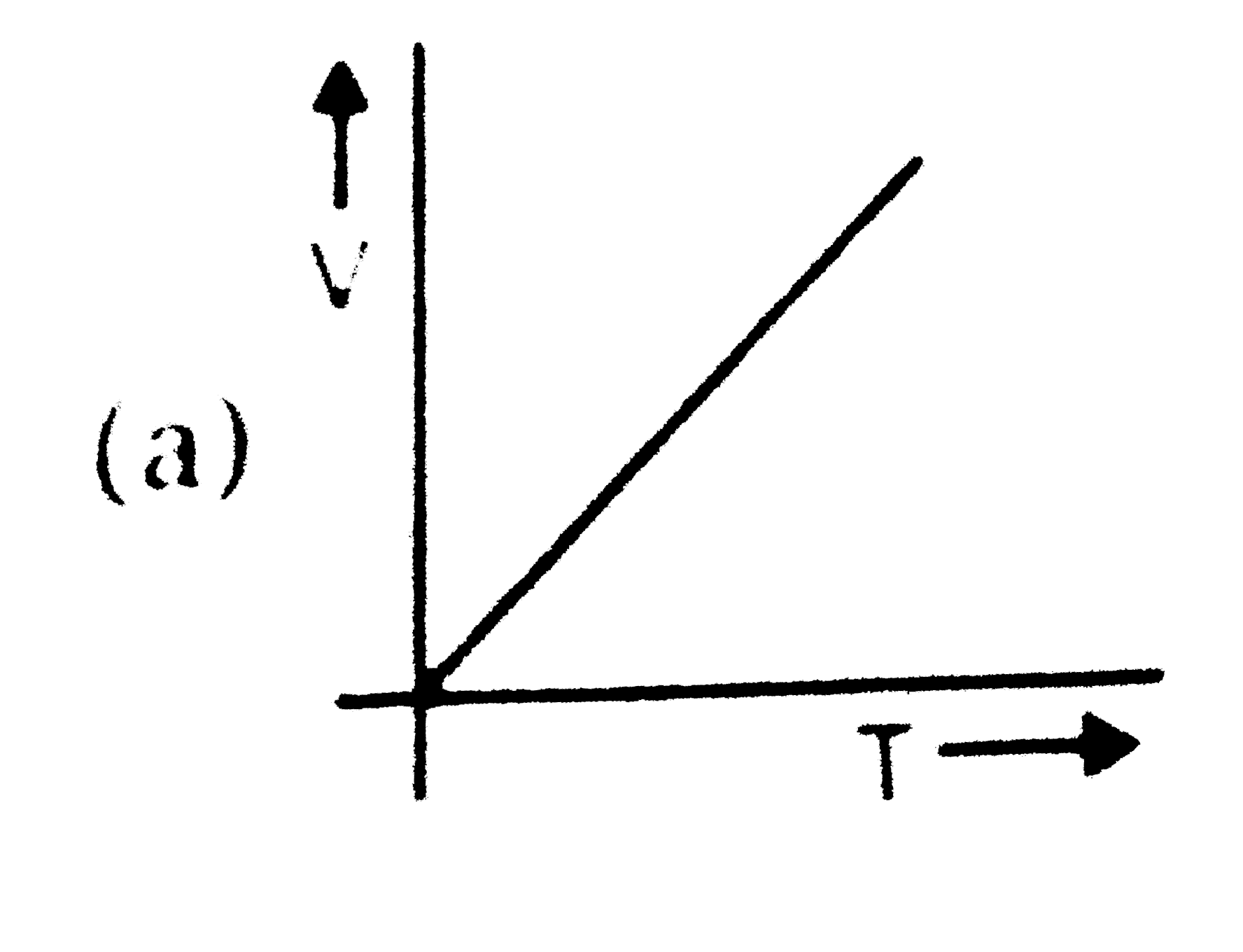
- Option A: If the graph shows a straight line passing through the origin (0,0), it represents V∝T. This is consistent with Charles's law.
- Option B: If the graph is of the form logV versus T, it can be expressed as:
logV=logk+logT
This is a linear relationship and will not pass through the origin, but it still represents a valid relationship.
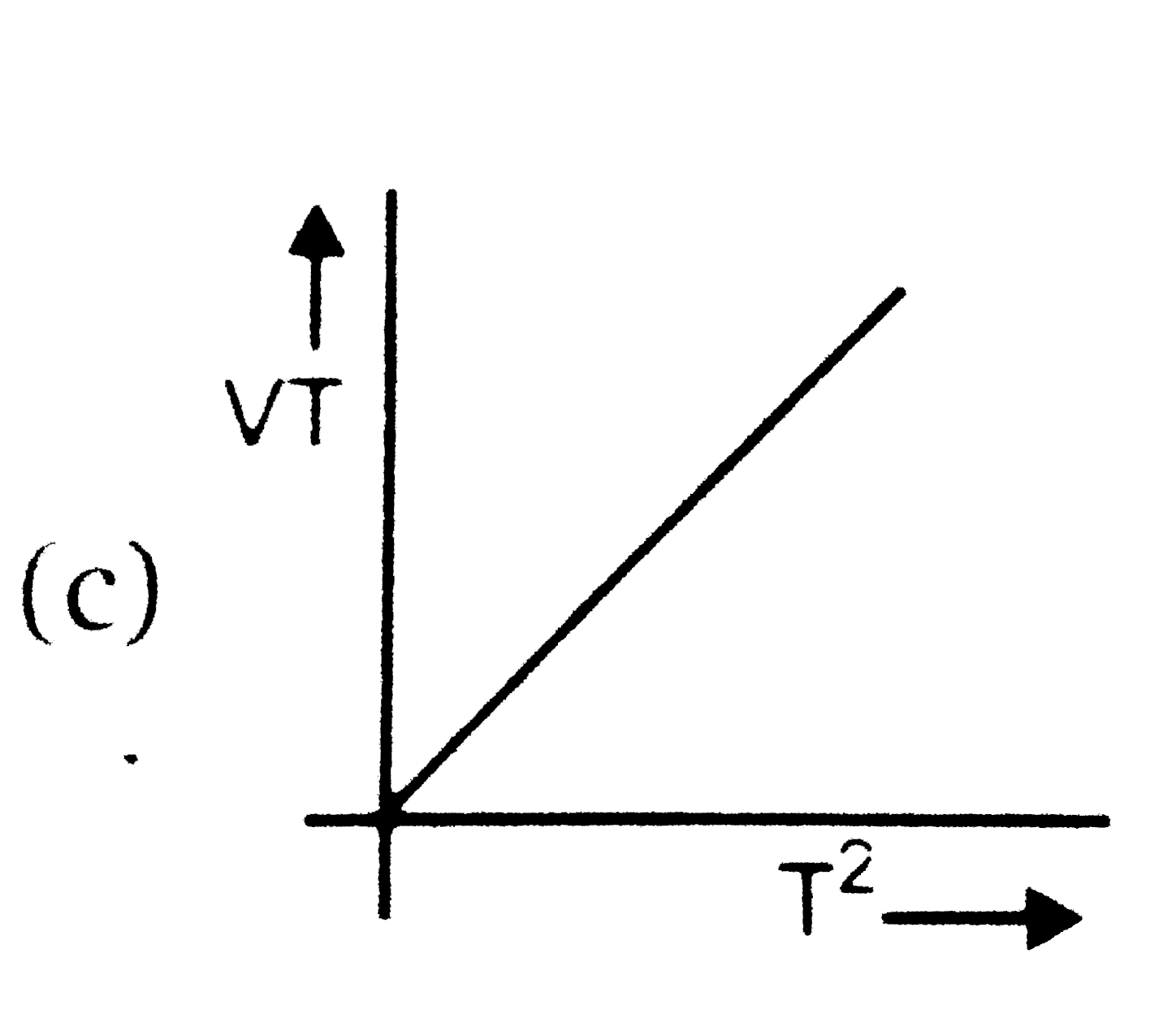
- Option C: If the graph is of the form V versus T2, it can be expressed as:
V∝T2
This is not consistent with Charles's law, which states that volume is directly proportional to temperature, not its square.
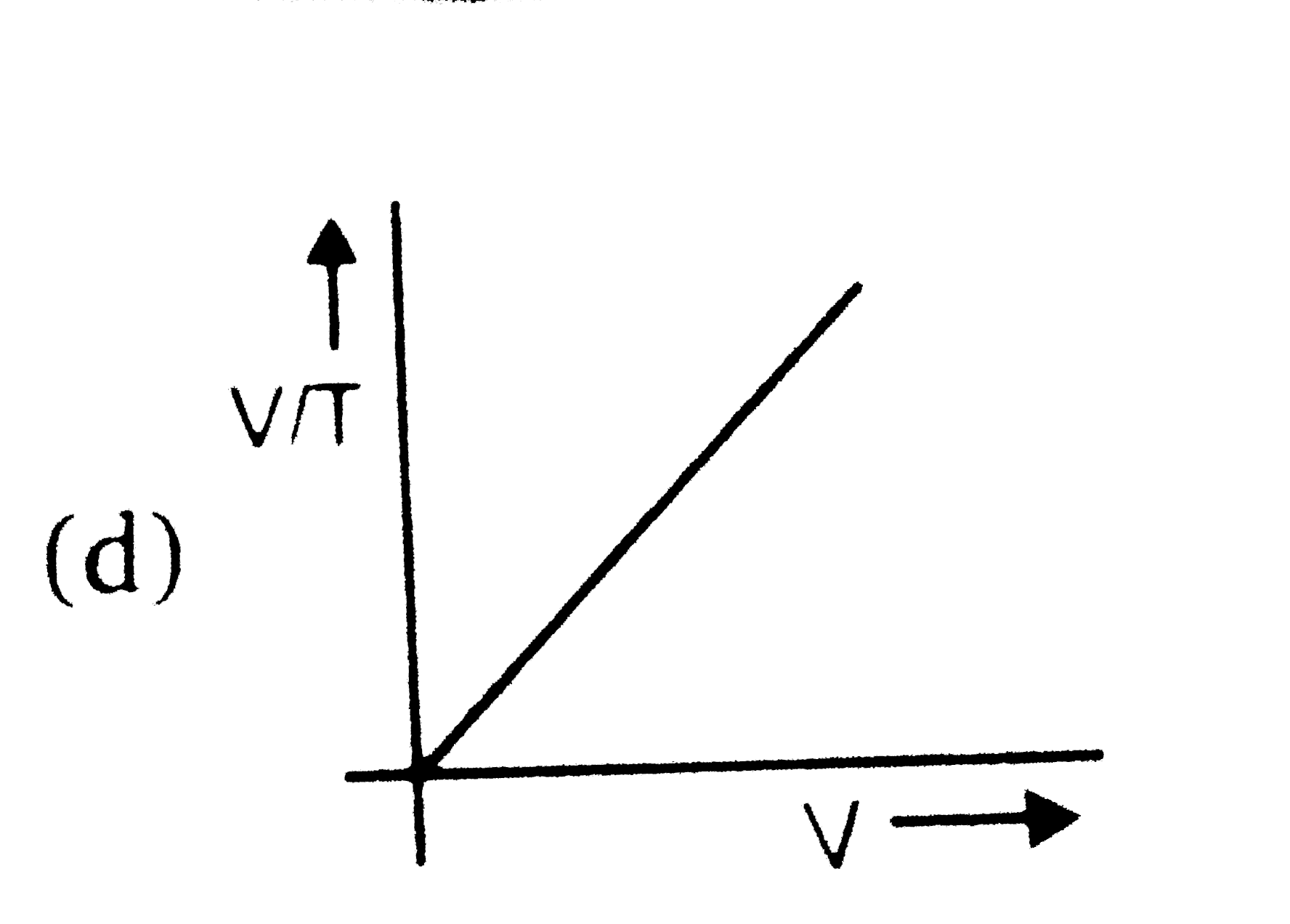
- Option D: If the graph shows V/T as a constant, it implies that the ratio V/T is constant, which is also a valid representation of Charles's law.
4. Conclusion:
- Among the options analyzed, Option C (which suggests a relationship of V∝T2) does not conform to Charles's law. Therefore, this is the correct answer.
Final Answer:
Option C is not according to Charles's law.
- Charles's law states that for a fixed amount of gas at constant pressure, the volume (V) of the gas is directly proportional to its absolute temperature (T). This can be mathematically expressed as:
V∝T(at constant pressure)
- This can also be written as:
V=kT
where k is a constant.
- We need to analyze the given options (curves) to see which one does not represent the relationship described by Charles's law.
- Option A: If the graph shows a straight line passing through the origin (0,0), it represents V∝T. This is consistent with Charles's law.
- Option B: If the graph is of the form logV versus T, it can be expressed as:
logV=logk+logT
This is a linear relationship and will not pass through the origin, but it still represents a valid relationship.
- Option C: If the graph is of the form V versus T2, it can be expressed as:
V∝T2
This is not consistent with Charles's law, which states that volume is directly proportional to temperature, not its square.
- Option D: If the graph shows V/T as a constant, it implies that the ratio V/T is constant, which is also a valid representation of Charles's law.
- Among the options analyzed, Option C (which suggests a relationship of V∝T2) does not conform to Charles's law. Therefore, this is the correct answer.
Option C is not according to Charles's law.
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 230videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 14videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Subjective problems14videos
ELECTROCHEMISTRY
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - IONIC EEQUILIBRIUMEXERCISE - Subjective problems1videos
IONIC EEQUILIBRIUM
Similar Questions
According to Charles's law
View SolutionAccording to charles's law,
 View Solution
View SolutionAccording to Boyle's law
View SolutionAccording to Wien's law
View SolutionAmong the following which is polar ? .
View SolutionAmong the following which is correct ?
View SolutionAmong the following, which is/are correct?
View SolutionState Charles.s law
View SolutionWhich of the following reactions isnot correct according to the law of conservation of mass?
View SolutionWhich of the following curves is correct?
View Solution
