Which of the following curves is correct?

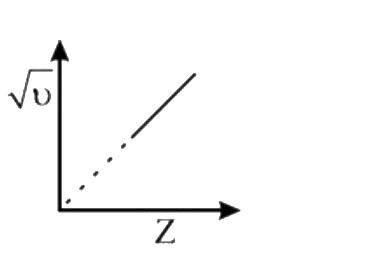
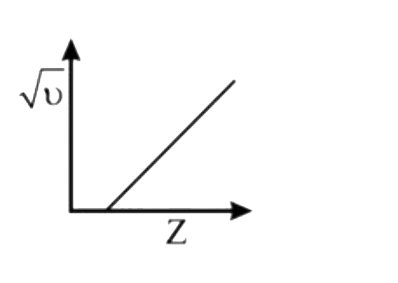
None of these
The correct Answer is:A
To solve the question regarding which of the given curves is correct based on the relationship between atomic number (z) and frequency (μ), we can follow these steps:
1. Understand the Variables:
- The x-axis represents the atomic number (z).
- The y-axis represents the square root of frequency (√μ).
2. Recall Moseley's Law:
- Moseley's Law states that the frequency (μ) of the characteristic X-rays emitted by an element is related to its atomic number (z) by the equation:
√μ=a(z−b)
- Here, a and b are constants.
3. Analyze the Equation:
- Rearranging the equation gives us:
√μ=az−ab
- This can be interpreted as a linear equation in the form of y=mx+c, where:
- y=√μ
- x=z
- m=a (slope)
- c=−ab (y-intercept)
4. Determine the Y-Intercept:
- The equation indicates that when z=b, √μ will be zero. However, since z cannot be less than b (as atomic numbers are positive integers), √μ will never actually reach zero for any element with a positive atomic number.
5. Evaluate the Options:
- Option 1: A curve that does not pass through the origin and has a positive y-intercept.
- Option 2: A curve that passes through the origin (which is incorrect since √μ cannot be zero).
- Option 3: A curve that approaches the x-axis but does not touch it.
6. Conclusion:
- Since √μ cannot be zero for any positive atomic number z, the correct curve must not pass through the x-axis. Therefore, the correct option is Option 1.
- The x-axis represents the atomic number (z).
- The y-axis represents the square root of frequency (√μ).
- Moseley's Law states that the frequency (μ) of the characteristic X-rays emitted by an element is related to its atomic number (z) by the equation:
√μ=a(z−b)
- Here, a and b are constants.
- Rearranging the equation gives us:
√μ=az−ab
- This can be interpreted as a linear equation in the form of y=mx+c, where:
- y=√μ
- x=z
- m=a (slope)
- c=−ab (y-intercept)
- The equation indicates that when z=b, √μ will be zero. However, since z cannot be less than b (as atomic numbers are positive integers), √μ will never actually reach zero for any element with a positive atomic number.
- Option 1: A curve that does not pass through the origin and has a positive y-intercept.
- Option 2: A curve that passes through the origin (which is incorrect since √μ cannot be zero).
- Option 3: A curve that approaches the x-axis but does not touch it.
- Since √μ cannot be zero for any positive atomic number z, the correct curve must not pass through the x-axis. Therefore, the correct option is Option 1.
Similar Questions
Knowledge Check
Which of the following curves is in accordance with Freundlich adsorption isotherm ?
A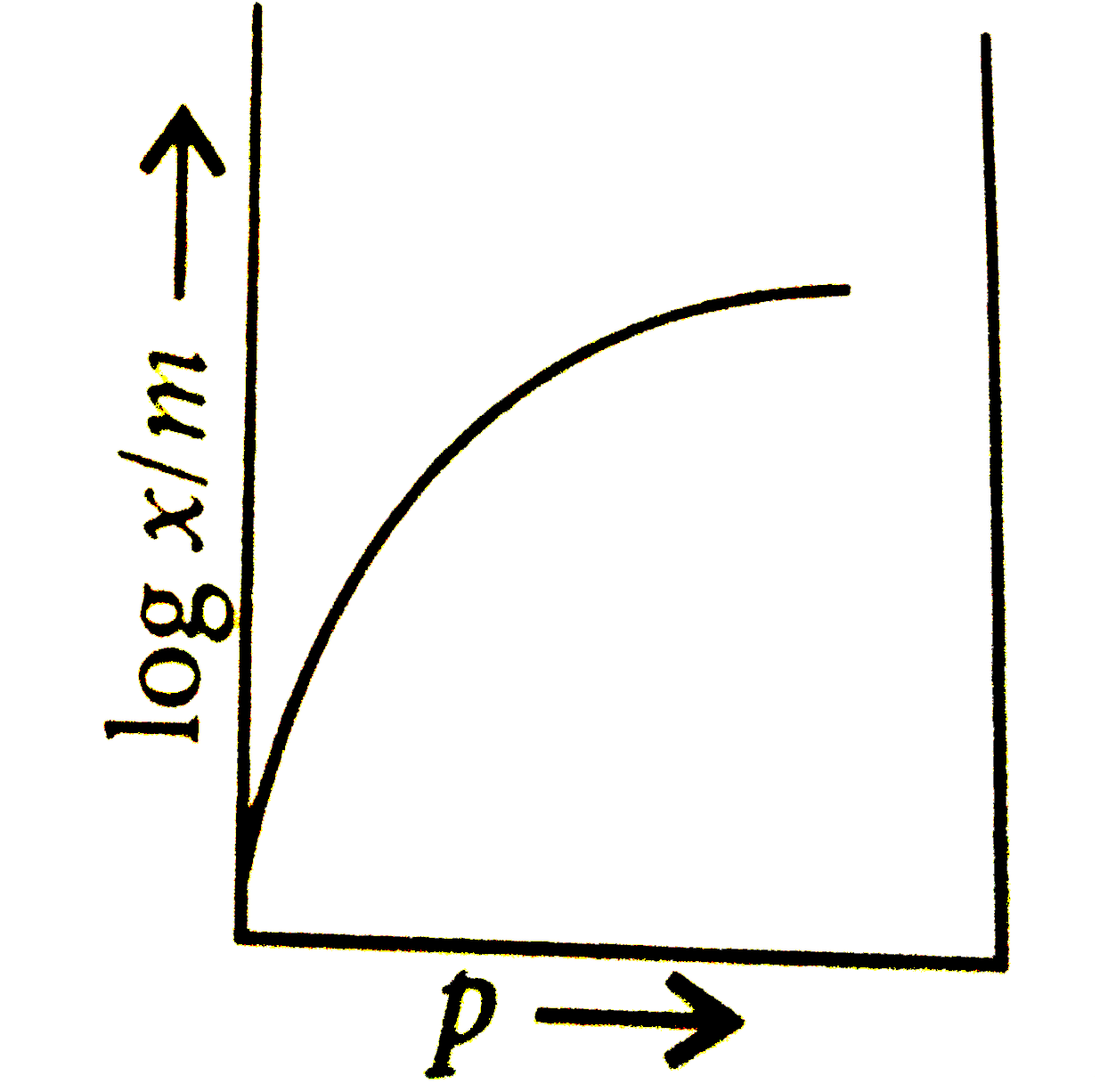 B
B C
C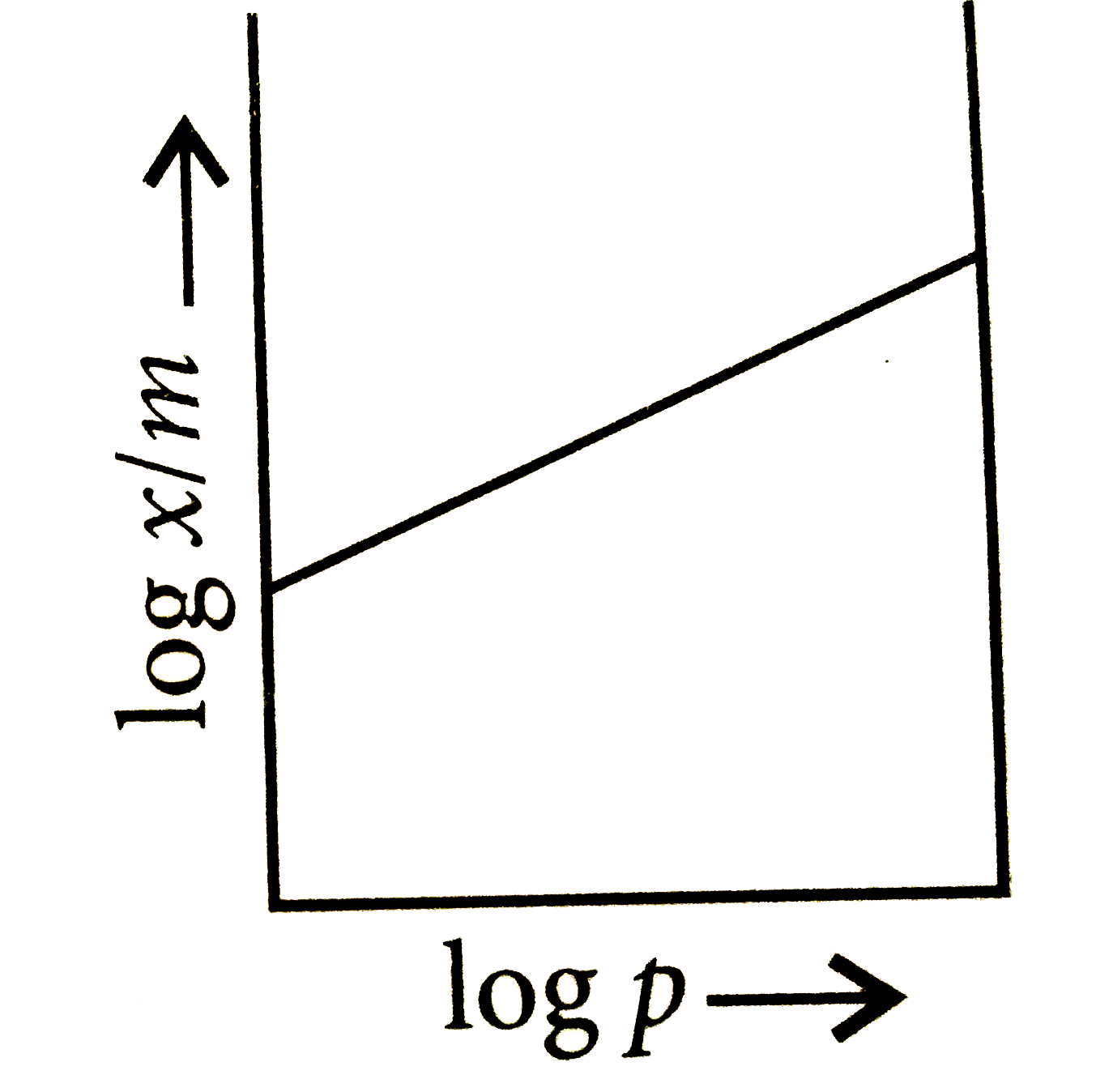 D
D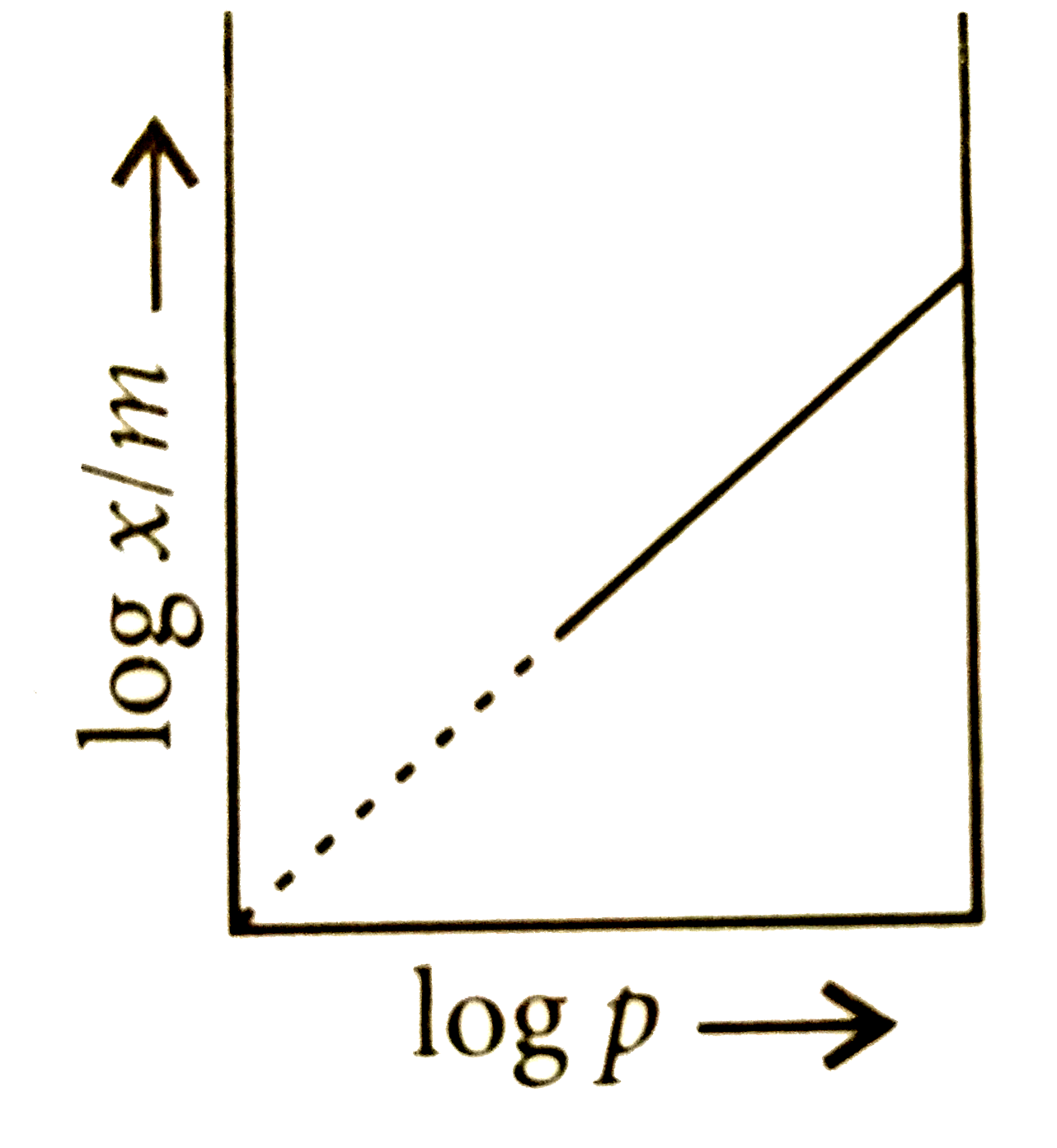
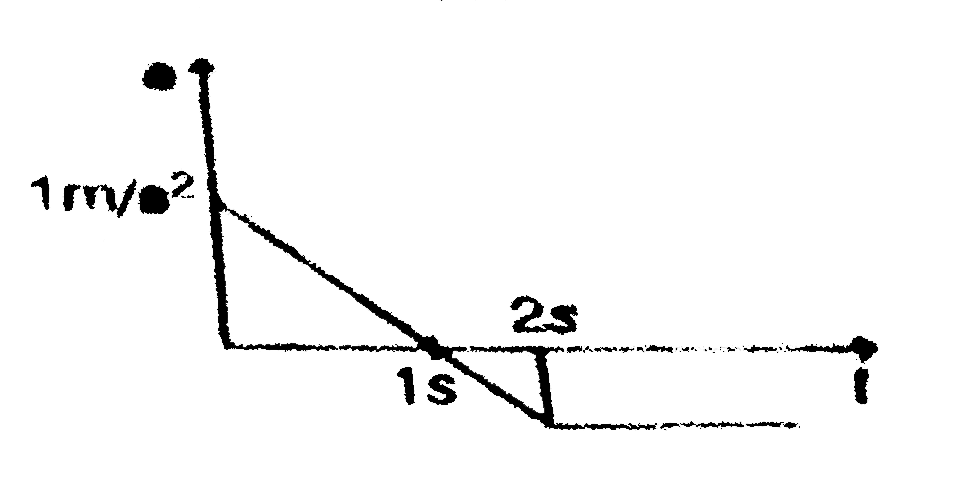
Acceleration versus time curve for a particle moving in a straight line is shown in the figure. If particle starts from rest at t=0, then which of the following curve is correct for the same particle.
View SolutionWhich of the following curves correctly represents the process of antibiotic production by Streptomyces sp ?
View SolutionShown below are the black body radiation curves at temperature T1 and T2(T2>T1). Which of the following plots is correct?
View SolutionWhich of the following match is correct ?
View SolutionWhich of the following curves corresponds to maximum growth ?
View SolutionWhich of the following curves is in according with Freundlich adsorption isotherm?
(a)
(b)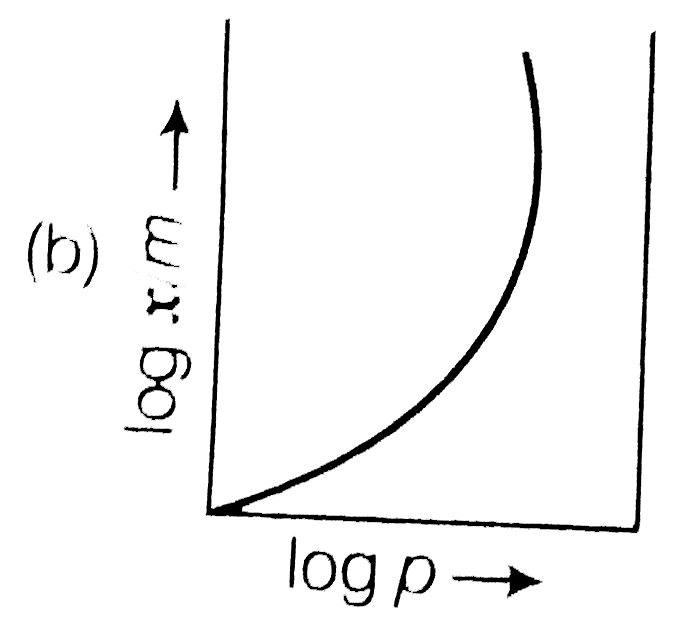
(c)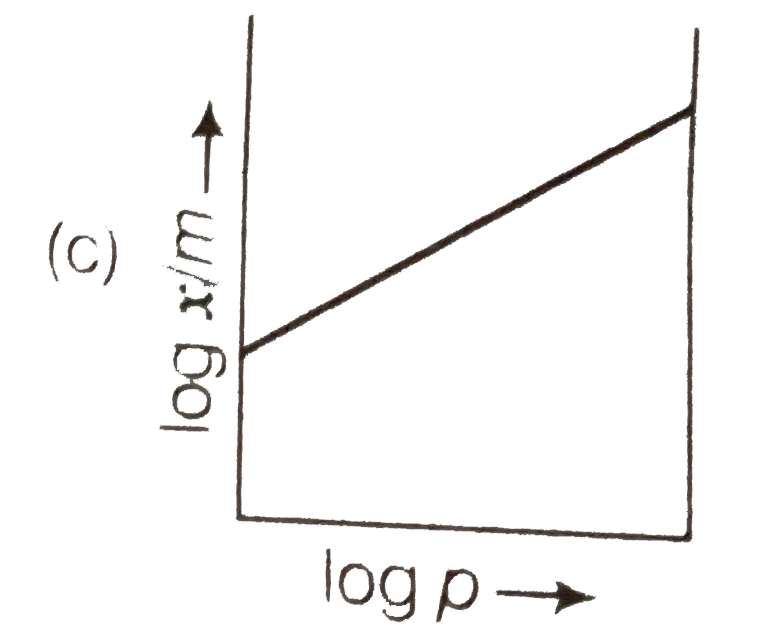
(d)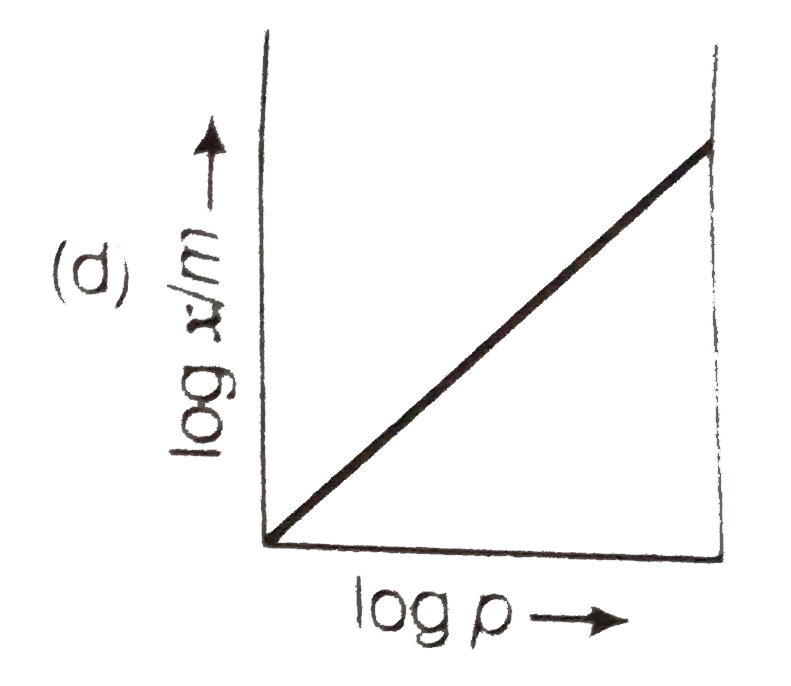
View SolutionFor radial probability curves. Which of the following is/are correct ?
View Solution
