Calculate λ of X-rays which give a diffraction angle 2θ=16.8∘ for crystal, if the interplanar distance in the crystal is 0.2nm and that only for the first-order diffraction is observed. Given sin8.40∘=0.146.
To calculate the wavelength (λ) of X-rays that give a diffraction angle of 2θ=16.8∘ for a crystal with an interplanar distance (d) of 0.2 nm, we will use Bragg's law, which is given by the formula:
nλ=2dsinθ
1. Identify the Given Values:
- The diffraction angle is given as 2θ=16.8∘.
- Therefore, θ=16.82=8.4∘.
- The interplanar distance d=0.2nm=0.2×10−9m.
- The order of diffraction n=1.
- We are also given that sin8.4∘=0.146.
2. Convert Interplanar Distance to Meters:
d=0.2nm=0.2×10−9m=2.0×10−10m
3. Apply Bragg's Law:
Substitute the known values into Bragg's law:
nλ=2dsinθ
Substituting n=1, d=2.0×10−10m, and sin8.4∘=0.146:
1λ=2×(2.0×10−10)×0.146
4. Calculate the Right Side:
λ=2×2.0×10−10×0.146
λ=4.0×10−10×0.146
λ=5.84×10−11m
5. Convert Wavelength to Nanometers:
To convert meters to nanometers, recall that 1nm=10−9m:
λ=5.84×10−11m=0.0584nm
Final Answer:
The wavelength of the X-rays is:
λ=5.84×10−11mor0.0584nm
- The diffraction angle is given as 2θ=16.8∘.
- Therefore, θ=16.82=8.4∘.
- The interplanar distance d=0.2nm=0.2×10−9m.
- The order of diffraction n=1.
- We are also given that sin8.4∘=0.146.
d=0.2nm=0.2×10−9m=2.0×10−10m
Substitute the known values into Bragg's law:
nλ=2dsinθ
Substituting n=1, d=2.0×10−10m, and sin8.4∘=0.146:
1λ=2×(2.0×10−10)×0.146
λ=2×2.0×10−10×0.146
λ=4.0×10−10×0.146
λ=5.84×10−11m
To convert meters to nanometers, recall that 1nm=10−9m:
λ=5.84×10−11m=0.0584nm
The wavelength of the X-rays is:
λ=5.84×10−11mor0.0584nm
Topper's Solved these Questions
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Solved Examples
13 Videos
- SOLID STATEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercises (Linked Comprehension)
13 Videos
- REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - REDUCTION AND OXIDATION REACTION OF ORGANIC COMPOUNDSEXERCISE - SUBJECTIVE TYPE
4 Videos
- SOLUTIONSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - SOLUTIONSEXERCISE - Ex 2.3 (Objective)
9 Videos
Similar Questions
The interplaner distance in a crystal is 2.8×10–8 m. The value of maximum wavelength which can be diffracted : -
View SolutionThe interplanar distance in a crystal used for X - ray diffraction is 2A0. The angle of incidence for first order diffraction is 9°, what is the wave length of X - rays?
View SolutionAssertion: Crystalline solids can cause X-rays to diffract.
Reason: Interatomic distance in crystalline solids is of the order of 0.1nm.
View SolutionWhen an electron in an excited state of Mo atoms falls from L to K-shell , an X-ray is emitted. These X-rays are diffracted at angle of 7.75∘ by planes with a separation of 2.94Ã…. What is the difference in energy between k-shell and L-shell in Mo, assuming of first order diffraction ? ( sin7.75∘=0.1349)
View SolutionA narrow neutron beam falls on a natural face of an aluminium single-crystal at a glancing angle of 5∘ The distance between crystallographic planes parallel to the single-crystal face is 0.20 nm. What is the velocity and the energy of neutrons for which a first-order maximum is observed in this direction? What is the temperature responding to this neutron velocity?
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
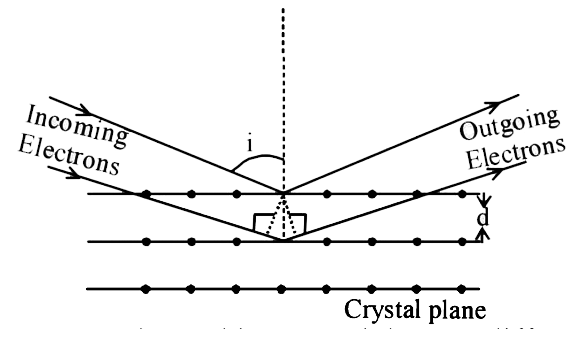
If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength λdB of electrons can be calculated by the relationship (n is an intenger)
View SolutionA sample of a crystalline solid scatters a beam of X-rays of wavelength 70.93 pm at an angle 2θ of 14.66∘. If this is a second-order reflection (n=2), calculate the distance between the parallel planers of atoms from which the scattered beam appears to have been reflected.
View SolutionFind the centre and the radius of the circles
x2+y2+2xsinθ+2ycosθ−8=0
View SolutionA first order reaction takes 40 minutes for 30% decomposition. Calculate t1/2 for this reaction (Given log 1.428 = 0.1548)
View SolutionA first order reaction takes 40 minutes for 30% decomposition. Calculate t1/2 for this reaction (Given log 1.428 = 0.1548)
View Solution
