Calculate the packing efficiency in simple cubic unit cell.

Text Solution

Verified by Experts

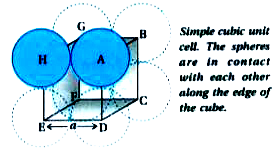
In a simple cubic unit cell, two spheres at the corners of the cube touch each other.
Let edge length of cube = a.
Let radius of sphere = r
The radius of sphere and edge length of cube is related as:
a = 2r
The volume of cubic unit cell $= a^{3} = {(2 r)}^{3} = 8 r^{3}$
Since the simple cubic unit cell contains only 1 atom, the volume of the occupied space is = $\frac{4}{3} π r^{3}$
% Packing efficiency = $\frac{Volume occupied by four spheres in unit cell \times 100}{Volume of the unit cell}$
$= \frac{4}{3} π r^{3}_(8 r^{3}) \times 100 = \frac{π}{6} \times 100$
$52.4 %$ .

Updated on:21/07/2023

Assertion (A) : Packing efficiency in simple cubic unit cell is $52.4 %$ .
Reason (R) : Density of the unit cell is given by the relation : $d = \frac{a^{3} N_{A}}{Z M}$ .
ABoth Assertion (A) and Reason (R) are correct statements, and Reason (R) is the correct explanation of the Assertion (A).
BBoth Assertion (A) and Reason (R) are correct statements, but Reason (R) is not the correct explanation of the Assertion (A).
CAssertion (A) is correct, but Reason (R) is incorrect statement.
DAssertion (A) is incorrect, but Reason (R) is correct statement.
The efficiency of packing in simple cubic unit cell is
A $\frac{π}{6}$
B $\frac{\sqrt{3} π}{8}$
C $\frac{\sqrt{2} π}{6}$
D $\frac{π}{16}$
The efficiency of packing in simple cubic unit cell is
A $\frac{π}{6}$
B $\frac{\sqrt{3} π}{8}$
C $\frac{\sqrt{2} π}{6}$
D $\frac{π}{16}$