Calculate the velocity of electron ejected from a platium surface when radiation of 200nm falls on it .The work function of platinum is 5eV(1eV=1.6×10−19J)
To calculate the velocity of an electron ejected from a platinum surface when radiation of 200 nm falls on it, we can follow these steps:
Step 1: Convert the wavelength from nanometers to meters
The wavelength (λ) is given as 200 nm. To convert this to meters:
λ=200nm=200×10−9m
Step 2: Calculate the energy of the incoming radiation
The energy (E) of the radiation can be calculated using the formula:
E=hcλ
Where:
- h=6.63×10−34J s (Planck's constant)
- c=3×108m/s (speed of light)
Substituting the values:
E=(6.63×10−34)×(3×108)200×10−9=9.945×10−19J
Step 3: Convert the work function from eV to Joules
The work function (Φ) of platinum is given as 5 eV. To convert this to Joules:
Φ=5eV×1.6×10−19J/eV=8.0×10−19J
Step 4: Calculate the kinetic energy of the ejected electron
Using Einstein's photoelectric equation:
KE=E−Φ
Substituting the values:
KE=9.945×10−19J−8.0×10−19J=1.945×10−19J
Step 5: Relate kinetic energy to velocity
The kinetic energy (KE) of the electron can also be expressed as:
KE=12mv2
Where:
- m=9.1×10−31kg (mass of an electron)
Rearranging for velocity (v):
v=√2×KEm
Substituting the values:
v=√2×1.945×10−199.1×10−31
Step 6: Calculate the velocity
Calculating the above expression:
v=√3.89×10−199.1×10−31=√4.28×1011≈6.54×105m/s
Final Answer
The velocity of the ejected electron is approximately:
v≈6.54×106m/s
The wavelength (λ) is given as 200 nm. To convert this to meters:
λ=200nm=200×10−9m
The energy (E) of the radiation can be calculated using the formula:
E=hcλ
Where:
- h=6.63×10−34J s (Planck's constant)
- c=3×108m/s (speed of light)
Substituting the values:
E=(6.63×10−34)×(3×108)200×10−9=9.945×10−19J
The work function (Φ) of platinum is given as 5 eV. To convert this to Joules:
Φ=5eV×1.6×10−19J/eV=8.0×10−19J
Using Einstein's photoelectric equation:
KE=E−Φ
Substituting the values:
KE=9.945×10−19J−8.0×10−19J=1.945×10−19J
The kinetic energy (KE) of the electron can also be expressed as:
KE=12mv2
Where:
- m=9.1×10−31kg (mass of an electron)
Rearranging for velocity (v):
v=√2×KEm
Substituting the values:
v=√2×1.945×10−199.1×10−31
Calculating the above expression:
v=√3.89×10−199.1×10−31=√4.28×1011≈6.54×105m/s
The velocity of the ejected electron is approximately:
v≈6.54×106m/s
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercises (Subjective)
52 Videos
- ATOMIC STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Exercises Linked Comprehension
50 Videos
- APPENDIX - INORGANIC VOLUME 1BOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - APPENDIX - INORGANIC VOLUME 1EXERCISE - chapter-7 Single correct answer
1 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Archives Subjective
15 Videos
Similar Questions
Energy required to stop the ejection of electrons from certain metal plate was found to be 0.2 eV when an electromagnetic radiation of 330 nm was made to fall on it the work function of the metal is
View SolutionRadiation falls on a target kept within a solenoid with 20 turns per cm, carrying a current 2.5 A. Electrons emitted move in a circle with a maximum radius of 1 cm. Find the wavelength of radiation, given that the work function of the target is 0.5 eV. q=1.6×10−19C, h=6.625×10−34J−s, mass of electron = 9.1×10−31kg
View SolutionThe photoelectric threshold wavelength of silver is 3250×10−10m. The velocity of the electron ejected from a silver surface by ultraviolet light of wavelength 2536×10−10m is
(Givenh=4.14×106ms−1eVs and c=3×108ms−1)
View SolutionThe photoelectric threshold wavelength of silver is 3250×10−10m. The velocity of the electron ejected from a silver surface by ultraviolet light of wavelength 2536×10−10m is
(Givenh=4.14×106ms−1eVs and c=3×108ms−1)
View SolutionFind the maximum velocity of photoelectrons emitted by radiation of frequency 3×1015 Hz from a photoelectric surface having a work function of 4.0 eV. Given h=6.6×10−34 Js and 1 eV = 1.6×10−19 J.
View SolutionCalculate the value of retarding potential in volt needed to stop the photoelectron ejected from a metal surface of work function 1.29 eV with light frequency of 5.5×1014sec−1 (nearly)
View SolutionFind the threshold wavelengths for photoelectric effect from a copper surface, a sodium surface and a cesium surface. The work functions of these metals are 4.5 eV, 2.3 eV and 1.9 eV respectively.
View SolutionThe work function of a metallic surface is 5.01eV. The photo - electrons are emitted when light of wavelength 2000 Å falls on it . The potential difference applied to stop the fastest photo - electrons is [h=4.14×10−15eVsec]
View Solution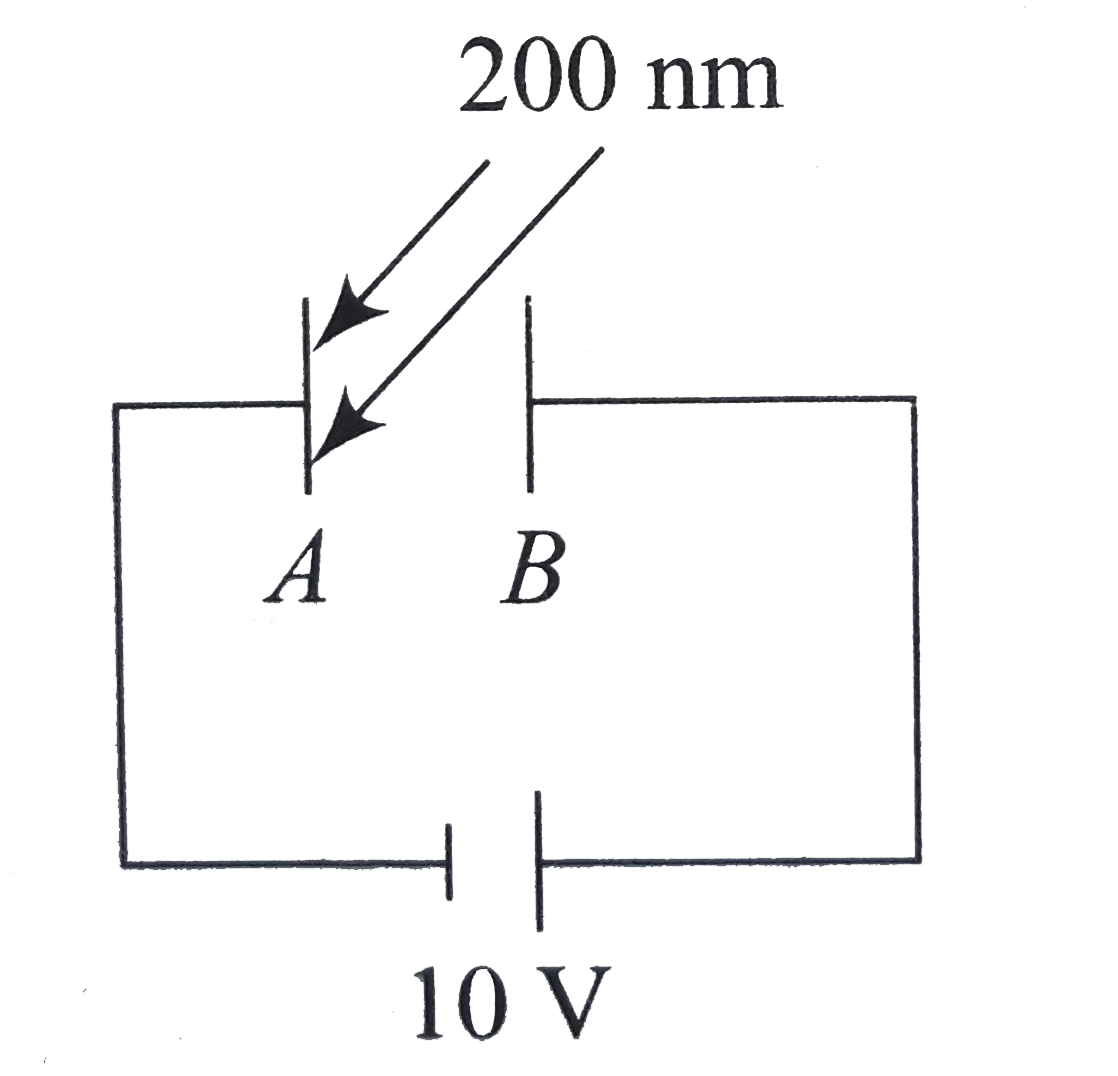
In Fig. electromagnetic radiations of wavelength 200nm are incident on a metallic plate A. the photoelectrons are accelerated by a potential difference of 10 V. These electrons strike another metal plate B from which electromagnetic radiations are emitted. The minimum wavelength of emitted photons is 100nm. If the work function of metal A is found to be (×x10−1)ev, then find the value of x. (Given hc=1240eV nm)
View SolutionCalculate the velocity of a photo-electron if the work function of the target material is 1.24eV and the wavelength of incident light is 4.36×10−7m. What retarding potential is necessary to stop the emission of the electrons?
View Solution
