Energy required to stop the ejection of electrons from certain metal plate was found to be 0.2 eV when an electromagnetic radiation of 330 nm was made to fall on it the work function of the metal is
0.32×10−19 j
6×10−19j
5.68×10−19 j
3.82×10−27
The correct Answer is:C
To find the work function of the metal, we can follow these steps:
Step 1: Understand the relationship between energy, work function, and kinetic energy
The energy of the incident photon (electromagnetic radiation) can be expressed as:
E=hν=hcλ
Where:
- E is the energy of the photon,
- h is Planck's constant (6.626×10−34Js),
- c is the speed of light (3.0×108m/s),
- λ is the wavelength of the radiation (in meters).
The kinetic energy (KE) of the emitted electrons is given as:
KE=E−Φ
Where:
- Φ is the work function of the metal.
Step 2: Convert the wavelength from nanometers to meters
Given the wavelength λ=330nm:
λ=330×10−9m
Step 3: Calculate the energy of the photon
Using the formula:
E=hcλ
Substituting the values:
E=(6.626×10−34Js)(3.0×108m/s)330×10−9m
Calculating this gives:
E=6.023×10−19J
Step 4: Convert the kinetic energy from eV to joules
The kinetic energy is given as 0.2eV. To convert this to joules:
KE=0.2eV×1.6×10−19J/eV=3.2×10−20J
Step 5: Rearrange the equation to find the work function
Using the equation:
Φ=E−KE
Substituting the values we calculated:
Φ=6.023×10−19J−3.2×10−20J
Calculating this gives:
Φ=5.703×10−19J
Step 6: Convert the work function from joules to eV
To convert the work function back to eV:
Φ=5.703×10−19J1.6×10−19J/eV≈3.56eV
Final Answer
The work function of the metal is approximately 3.56eV.
---
The energy of the incident photon (electromagnetic radiation) can be expressed as:
E=hν=hcλ
Where:
- E is the energy of the photon,
- h is Planck's constant (6.626×10−34Js),
- c is the speed of light (3.0×108m/s),
- λ is the wavelength of the radiation (in meters).
KE=E−Φ
Where:
- Φ is the work function of the metal.
Given the wavelength λ=330nm:
λ=330×10−9m
Using the formula:
E=hcλ
Substituting the values:
E=(6.626×10−34Js)(3.0×108m/s)330×10−9m
Calculating this gives:
E=6.023×10−19J
The kinetic energy is given as 0.2eV. To convert this to joules:
KE=0.2eV×1.6×10−19J/eV=3.2×10−20J
Using the equation:
Φ=E−KE
Substituting the values we calculated:
Φ=6.023×10−19J−3.2×10−20J
Calculating this gives:
Φ=5.703×10−19J
To convert the work function back to eV:
Φ=5.703×10−19J1.6×10−19J/eV≈3.56eV
The work function of the metal is approximately 3.56eV.
Topper's Solved these Questions
- STRUCTURE OF ATOMBOOK - VMC MODULES ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - ENABLE
50 Videos
- STRUCTURE OF ATOMBOOK - VMC MODULES ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - EFFICIENT
48 Videos
- STOICHIOMETRY-IIBOOK - VMC MODULES ENGLISHCHAPTER - STOICHIOMETRY-IIEXERCISE - JEE Advanced (Archive)
43 Videos
- SURFACE CHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - PRACTICE EXERCISE
9 Videos
Similar Questions
The energy required to stop ejection of electrons from a Cu plate is 0.24eV .Calculate the work function Cu when a radiation of wavelength λ=250 nm strikes the plate
View SolutionEjection of the photoelectron from metal in the photoelectric effect experiment can be stopped by applying 0.5 V when the radiation of 250 nm is used. The work function of the metal is
View SolutionThe kinetic energy of most energetic electrons emitted from a metallic surface is doubled when the wavelength λ of the incident radiation is changed from 400 nm to 310 nm. The work function of the metal is
View Solution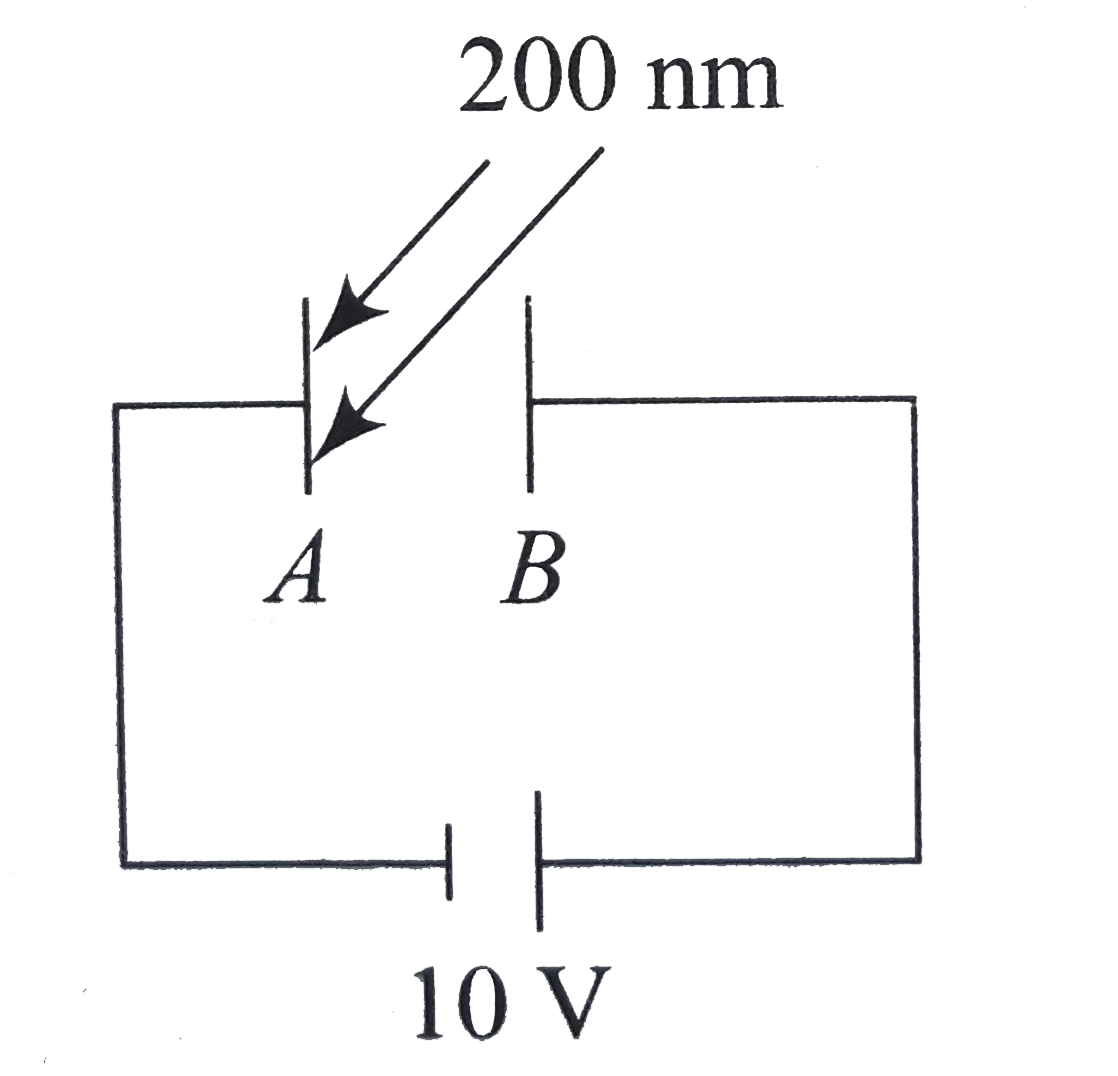
In Fig. electromagnetic radiations of wavelength 200nm are incident on a metallic plate A. the photoelectrons are accelerated by a potential difference of 10 V. These electrons strike another metal plate B from which electromagnetic radiations are emitted. The minimum wavelength of emitted photons is 100nm. If the work function of metal A is found to be (×x10−1)ev, then find the value of x. (Given hc=1240eV nm)
View SolutionThe maximum kinetic energy of photoelectrons emitted from a metal surface increses from 0.4 eV to 1.2 eV when the frequency of the incident radiation is increased by 40% . What is the work function (in eV) of the metal surface?
View SolutionThe work function of a metal is 3.4 eV. If the frequency of incident radiation is increased to twice, then the work function of the metal becomes.
View SolutionThe threshold wavelength for ejection of electrons from a metal is 330 nm. The work function for the photoelectric emission from the metal is
View SolutionThe threshold wavelength for ejection of electrons from a metal is 430 nm. The work function for the photoelectric emission from the metal is
View SolutionThe threshold wavelength for ejection of electrons from a metal is 250 nm. The work function for the photoelectric emission from the metal is
View SolutionThe threshold wavelength for ejection of electrons from a metal is 300 nm. The work function for the photoelectric emission from the metal is
View Solution
