ColumnI(Shell)ColumnII(Value of l)(A)2nd(P)1(B)3rd(Q)2(C)4th(R)3(D)1st(S)0
To solve the question regarding the relationship between the shells and their corresponding azimuthal quantum numbers (l), we will analyze each shell one by one.
1. Understanding Quantum Numbers:
- The principal quantum number (n) indicates the shell of an electron.
- The azimuthal quantum number (l) can take values from 0 to (n-1).
2. Analyzing the First Option (2nd Shell):
- For the 2nd shell, n = 2.
- The possible values of l are from 0 to (2-1) = 1.
- Therefore, the values of l for the 2nd shell are: 0 (s orbital) and 1 (p orbital).
- Match: (A) 2nd shell → (S) 0, (P) 1.
3. Analyzing the Second Option (3rd Shell):
- For the 3rd shell, n = 3.
- The possible values of l are from 0 to (3-1) = 2.
- Therefore, the values of l for the 3rd shell are: 0 (s orbital), 1 (p orbital), and 2 (d orbital).
- Match: (B) 3rd shell → (S) 0, (P) 1, (Q) 2.
4. Analyzing the Third Option (4th Shell):
- For the 4th shell, n = 4.
- The possible values of l are from 0 to (4-1) = 3.
- Therefore, the values of l for the 4th shell are: 0 (s orbital), 1 (p orbital), 2 (d orbital), and 3 (f orbital).
- Match: (C) 4th shell → (S) 0, (P) 1, (Q) 2, (R) 3.
5. Analyzing the Fourth Option (1st Shell):
- For the 1st shell, n = 1.
- The possible values of l are from 0 to (1-1) = 0.
- Therefore, the only value of l for the 1st shell is: 0 (s orbital).
- Match: (D) 1st shell → (S) 0.
Final Matches:
- (A) 2nd shell → (S) 0, (P) 1
- (B) 3rd shell → (S) 0, (P) 1, (Q) 2
- (C) 4th shell → (S) 0, (P) 1, (Q) 2, (R) 3
- (D) 1st shell → (S) 0
- The principal quantum number (n) indicates the shell of an electron.
- The azimuthal quantum number (l) can take values from 0 to (n-1).
- For the 2nd shell, n = 2.
- The possible values of l are from 0 to (2-1) = 1.
- Therefore, the values of l for the 2nd shell are: 0 (s orbital) and 1 (p orbital).
- Match: (A) 2nd shell → (S) 0, (P) 1.
- For the 3rd shell, n = 3.
- The possible values of l are from 0 to (3-1) = 2.
- Therefore, the values of l for the 3rd shell are: 0 (s orbital), 1 (p orbital), and 2 (d orbital).
- Match: (B) 3rd shell → (S) 0, (P) 1, (Q) 2.
- For the 4th shell, n = 4.
- The possible values of l are from 0 to (4-1) = 3.
- Therefore, the values of l for the 4th shell are: 0 (s orbital), 1 (p orbital), 2 (d orbital), and 3 (f orbital).
- Match: (C) 4th shell → (S) 0, (P) 1, (Q) 2, (R) 3.
- For the 1st shell, n = 1.
- The possible values of l are from 0 to (1-1) = 0.
- Therefore, the only value of l for the 1st shell is: 0 (s orbital).
- Match: (D) 1st shell → (S) 0.
- (A) 2nd shell → (S) 0, (P) 1
- (B) 3rd shell → (S) 0, (P) 1, (Q) 2
- (C) 4th shell → (S) 0, (P) 1, (Q) 2, (R) 3
- (D) 1st shell → (S) 0
Similar Questions
Match the following :
Column-IColumn-II(A)3s1(p)n=3(B)3p1(q)l=0(C)4s1(r)l=1(D)4d1(s)m=0(t)m=±1
View SolutionColumnIColumnII(A)K.E.P.E.(P)2(B)P.E+2K.E.(Q)−12(C)P.E.T.E.(R)1(D)K.E.T.E.(S)0
View SolutionIn case of hydrogen spectrum wave number is given by
¯v=RH[1n21−1n22] where n1>n2
ColumnIColumnII(A)Lyman series(P)n2=2(B)Balmer series(Q)n2=3(C)Pfund series(R)n2=6(D)Brackett series(S)n2=5
View SolutionMatch Column - I with Column - II
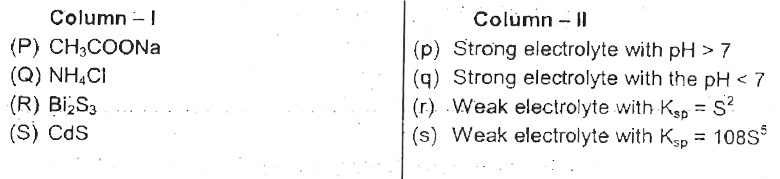
PQRS(A)1243(B)2143(C)4132(D)4321
View SolutionMeasured valueSignificant figures(A)0.0235(P)5(B)235×102(Q)4(C)46.64÷2.3(R)3(D)234.0(S)2
View Solutionmatch the following .
columnIcolumnII(i)4.1.14.116(a)AP(ii)2.3.5.7(b)sequence (iii)13.8.3.−2.−7(c)GP
View SolutionColumnIColumnII(A)The d-orbital which has two angular nodes(P)3dx2−y2(B)The d-orbitial with two nodal surfaced from conce(Q)3ds2(C)The orbital without angular node(R)4f(D)The orbital which has three angular nodes(S)3s
View SolutionColumnIColumnII(A)Orbital angular momentum of an electron(P)√s(s+1)h2π(B)Angular momentum of an electron in an orbit(Q)√(n(n+2))(C)Spin angular momentum of an electron(R)nh2π(D)Magnetic moment of atom(S)√(l(l+1)h2π)
View SolutionMatch the following

PQRS(A)1243(B)2143(C)4132(D)4321
View SolutionColumnIColumnII(A)Number of orbitials in thenthshell(P)2(2l+1)(B)Maximum number of electrons in a subshell(Q)n(C)Number of subshell innthshell(R)2l+1(D)Number of orbitals in a subshell(S)n2
View Solution
