Match the following :
Column-IColumn-II(A)3s1(p)n=3(B)3p1(q)l=0(C)4s1(r)l=1(D)4d1(s)m=0(t)m=±1
The correct Answer is:A(p,q,s),B(p,r,s,t),C(q,s),D(s,t)
To solve the question of matching the quantum numbers from Column I with the corresponding descriptions in Column II, we will analyze each entry step by step.
1. Identify Quantum Numbers for 3s¹ (A):
- The principal quantum number (n) for 3s¹ is 3.
- The azimuthal quantum number (l) for s subshell is 0.
- The magnetic quantum number (m) can only be 0 (since for l=0, m can only be 0).
- Match: A (3s¹) matches with (p) where n=3 and (q) where l=0, and (s) where m=0.
2. Identify Quantum Numbers for 3p¹ (B):
- The principal quantum number (n) for 3p¹ is 3.
- The azimuthal quantum number (l) for p subshell is 1.
- The possible magnetic quantum numbers (m) for l=1 are -1, 0, +1.
- Match: B (3p¹) matches with (p) where n=3 and (r) where l=1, and (t) where m=±1.
3. Identify Quantum Numbers for 4s¹ (C):
- The principal quantum number (n) for 4s¹ is 4.
- The azimuthal quantum number (l) for s subshell is 0.
- The magnetic quantum number (m) can only be 0.
- Match: C (4s¹) matches with (q) where l=0 and (s) where m=0.
4. Identify Quantum Numbers for 4d¹ (D):
- The principal quantum number (n) for 4d¹ is 4.
- The azimuthal quantum number (l) for d subshell is 2.
- The possible magnetic quantum numbers (m) for l=2 are -2, -1, 0, +1, +2.
- Match: D (4d¹) matches with (s) where m=0 and (t) where m=±1.
Final Matches:
- A (3s¹) matches with (p), (q), and (s).
- B (3p¹) matches with (p), (r), and (t).
- C (4s¹) matches with (q) and (s).
- D (4d¹) matches with (s) and (t).
Summary of Matches:
- A → p, q, s
- B → p, r, t
- C → q, s
- D → s, t
- The principal quantum number (n) for 3s¹ is 3.
- The azimuthal quantum number (l) for s subshell is 0.
- The magnetic quantum number (m) can only be 0 (since for l=0, m can only be 0).
- Match: A (3s¹) matches with (p) where n=3 and (q) where l=0, and (s) where m=0.
- The principal quantum number (n) for 3p¹ is 3.
- The azimuthal quantum number (l) for p subshell is 1.
- The possible magnetic quantum numbers (m) for l=1 are -1, 0, +1.
- Match: B (3p¹) matches with (p) where n=3 and (r) where l=1, and (t) where m=±1.
- The principal quantum number (n) for 4s¹ is 4.
- The azimuthal quantum number (l) for s subshell is 0.
- The magnetic quantum number (m) can only be 0.
- Match: C (4s¹) matches with (q) where l=0 and (s) where m=0.
- The principal quantum number (n) for 4d¹ is 4.
- The azimuthal quantum number (l) for d subshell is 2.
- The possible magnetic quantum numbers (m) for l=2 are -2, -1, 0, +1, +2.
- Match: D (4d¹) matches with (s) where m=0 and (t) where m=±1.
- A (3s¹) matches with (p), (q), and (s).
- B (3p¹) matches with (p), (r), and (t).
- C (4s¹) matches with (q) and (s).
- D (4d¹) matches with (s) and (t).
- A → p, q, s
- B → p, r, t
- C → q, s
- D → s, t
Topper's Solved these Questions
- STRUCTURE OF ATOM BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRUCTURE OF ATOM EXERCISE - ASSIGNMENT ( SECTION -G) Integer Answer Type Questions
4 Videos
- STRUCTURE OF ATOM BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRUCTURE OF ATOM EXERCISE - ASSIGNMENT ( SECTION -H) Multiple True - False Type Questions
5 Videos
- STRUCTURE OF ATOM BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRUCTURE OF ATOM EXERCISE - ASSIGNMENT ( SECTION -E) Assertion - Reason Type Questions
10 Videos
- STRUCTURE OF ATOMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRUCTURE OF ATOMEXERCISE - ASSIGNMENT (SECTION -D) Assertion-Reason Type Questions
15 Videos
- SURFACE CHEMISTRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SURFACE CHEMISTRY EXERCISE - Assignment Section - C (Assertion - Reason type questions)
10 Videos
Similar Questions
Four rods of equal length l and mass m each forms a square as shown in figure
Moment of inertia about three axes 1,2 and 3 are say I1,I2andI3. Then, match the following columns

Column-IColumn-II(A)I1(p)43ml2(B)I2(q)23ml2(C)I3(r)12ml2(s)None
View Solution√v versus Z graph for characteristic X-rays is as shown in figure. Match the following :
_E01_127_Q01.png)
Column IColumn II(A)Line-1(p)Lα(B)Line-2(q)Lβ(C)Line-3(r)Kα(D)Line-4(s)Kβ.
View SolutionMatch the followingColumn -IColumn -II(A)H3PO3(p)m=2.79 mol/kg(B)20 vol . of H2O2(q)M=2.31 molL−1(C)3 M NaCl solution with d=1.25gcm−3(r)1.7 mol L−1(D)Mole fraction of ethanol inH2O=0.04(s)Dibasic (t)3.4N
View SolutionMatch Column - I with Column - II
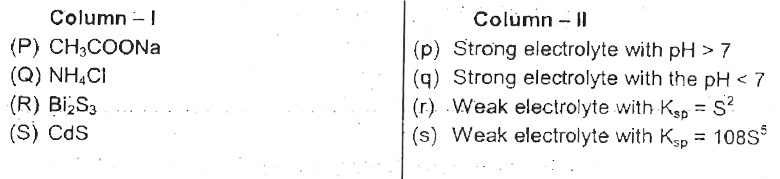
PQRS(A)1243(B)2143(C)4132(D)4321
View SolutionColumn IColumn II(A)R/L(p)Time(B)C/R(q)Frequency(C)E/B(r)Speed(D)√ε0μ0(s)None
View SolutionColumnI(Shell)ColumnII(Value of l)(A)2nd(P)1(B)3rd(Q)2(C)4th(R)3(D)1st(S)0
View SolutionMatch the following

PQRS(A)1243(B)2143(C)4132(D)4321
View SolutionIn the circuit shown in figure, E = 10 V, r = 1Ω,
R = 4Ω and L = 5H. The circuit is closed at time t = 0.
Then, match the following two columns.
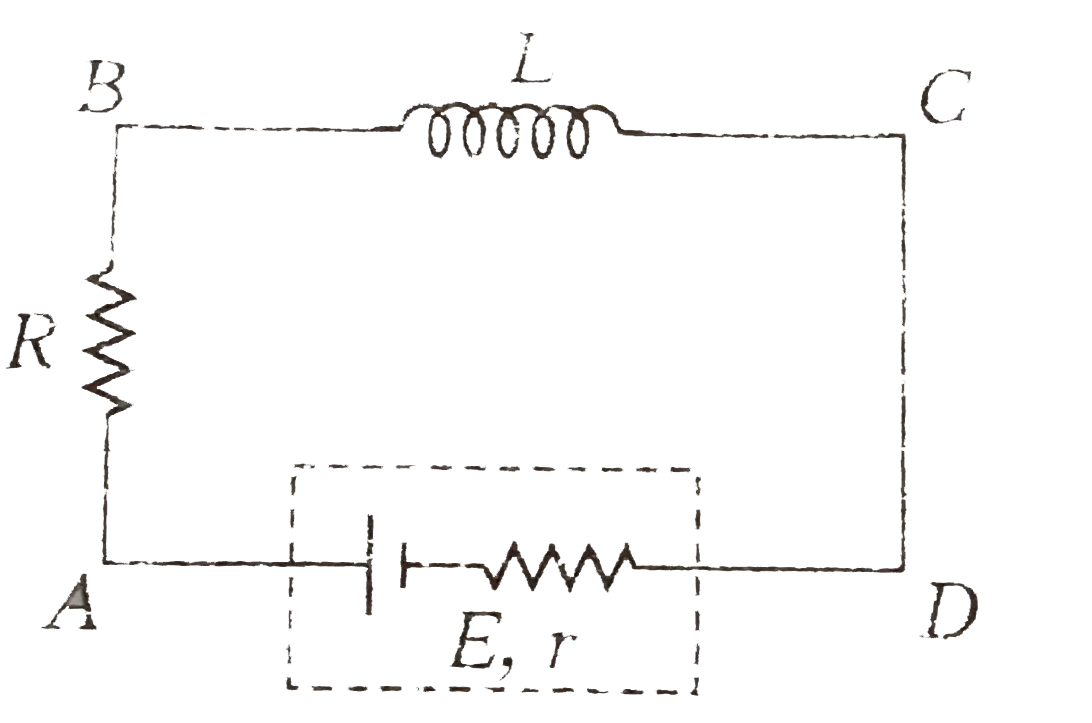
Column IColumn IIA.VAD at t = 0p4VB.VBC at t = 0q8VC.VAB at t =∞r.0VD.VAD at t=∞s.10V
View SolutionMatch the following columns.
Column IColumn IIA.Teslap[ML2A−2T−2]B.Weberq[MLA−2T−1]C.Weber m−2r.[MA−1T−2]D.Henrys.None
View SolutionThere are four vernier scales, whose observations are given in column - I and the correcponding calculations of least count are given in column - II. Match column - I with column - II appropriately. (Here S = value of IMSD : N = Value of number of divisions on vernier) (Assume ideal conditions)
Column - IColumn - II(A)S=1mm:N=10(P)0.05mm(B)S=0.5mm:N=10(Q)0.01mm(C)S=0.5mm:N=20(R)0.1mm(D)S=1mm:N=100(S)0.025mm
View Solution
