Consider the following Borh-Habber's cycle for formation of MX3(s).
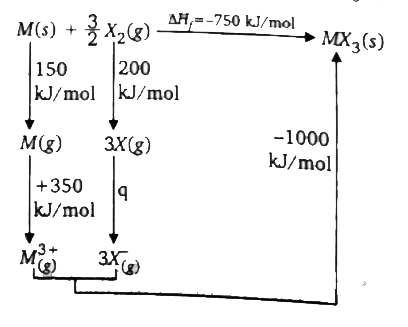
Then calculate value q150, here q1 is electron affinity of X(g) in kJ/mol.
The correct Answer is:4
−750=150+32×200+350+q−1000
q=3×ΔHBG=−550,
q1=5503=183,q150=3.66≈4.0
Topper's Solved these Questions
- BOOK - VK JAISWAL ENGLISHCHAPTER - PERIODIC PROPERTIESEXERCISE - Level 2102videos
PERIODIC PROPERTIES
- BOOK - VK JAISWAL ENGLISHCHAPTER - PERIODIC PROPERTIESEXERCISE - MATCH THE COLUMN11videos
PERIODIC PROPERTIES
- BOOK - VK JAISWAL ENGLISHCHAPTER - PERIODIC PROPERTIESEXERCISE - ASSERTION-REASON TYPE QUESTIONS36videos
PERIODIC PROPERTIES
- BOOK - VK JAISWAL ENGLISHCHAPTER - p-BLOCK ELEMENTSEXERCISE - SUBJECTIVE PROBLEMS35videos
p-BLOCK ELEMENTS
- BOOK - VK JAISWAL ENGLISHCHAPTER - QUALITATIVE INORGANIC ANALYSISEXERCISE - SUBJECTIVE PROBLEMS4videos
QUALITATIVE INORGANIC ANALYSIS
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following has the least electron affinity in kJmol−1?
AOxygenBcarbonCNitrogenDBoron - Question 2 - Select One
Which of the following are the values of electron affinities in kJ/mol for the formation of O− and O2− from O?
A-142, -702B-141, 702C142, 702D−142,−142
Consider the following table

Then calculate value of "p+q+r-s-t".View SolutionCalculate Q1,Q2andQ3,
 View Solution
View SolutionFor an ionic solid MX2, where X is monovalent, the enthalpy of formation of the enthalpy of formation of the solid from M (s) and X2(g) is 1.5 times the electron gain enthalpy of X(g). The first and second ionisation enthalpies of the meta (M) are 1.2 and 2.8 times of the enthalpy of sublimation of M(s). The bond dissociation enthalpy of X2(g) is 0.8 times the first ionisation enthalpy of metal and it is also equal to one -fifth of the magnitude of lattice enthalpy of MX2. If the electron gain enthalpy of X(g) is −96Kcal/mol, the answer the enthalpy of sublimation of metal (M) in K cal/mol
View SolutionCalculate the lattice enthalpy of KCl from the following data by Born- Haber's Cycle.
Enthalpy of sublimation of K=89kJmol–1
Enthalpy of dissociation of Cl=244kJmol–1
Ionization enthalpy of potassium = 425kJmol–1
Electron gain enthalpy of chlorine = –355kJmol–1
Enthalpy of formation of KCl=–438kJmol−1View SolutionThe ΔH0f(KF,s) is −563kJmol−1. The ionization enthalpy of K(g) is 419kJmol−1. and the enthalpy of sublimation of potassium is 88kJmol−1. The electron affinity of F(g) is 322kJmol−1 and F−F bond enthalpy is 158kJmol_1. Calculate the lattice enthalpy of KF(s).
The given data are as follows:
(i) K(s)+1/2F2(g)→KF(s) ΔH0f=−563kJmol−1
(ii) K(g)→K+(g)+e− Δ0Ioniz=419kJmol−1
(iii) K(s)→K(g) ΔH0sub=88kJmol−1
(iv) F(g)+e−→F−(g) ΔH0eg=−322kJmol−1
(v) F2(g)→2F(s) ΔH0diss=158kJmol−1
(vi) K+(g)+F−(g)→KF(s) ΔH0L=?View SolutionThe ΔH0f(KF,s) is −563kJmol−1. The ionization enthalpy of K(g) is 419kJmol−1. and the enthalpy of sublimation of potassium is 88kJmol−1. The electron affinity of F(g) is 322kJmol−1 and F−F bond enthalpy is 158kJmol_1. Calculate the lattice enthalpy of KF(s).
The given data are as follows:
(i) K(s)+1/2F2(g)→KF(s) ΔH0f=−563kJmol−1
(ii) K(g)→K+(g)+e− Δ0Ioniz=419kJmol−1
(iii) K(s)→K(g) ΔH0sub=88kJmol−1
(iv) F(g)+e−→F−(g) ΔH0eg=−322kJmol−1
(v) F2(g)→2F(s) ΔH0diss=158kJmol−1
(vi) K+(g)+F−(g)→KF(s) ΔH0L=?View Solution

