Energy of electron varies with atomic number as the following curve/line:
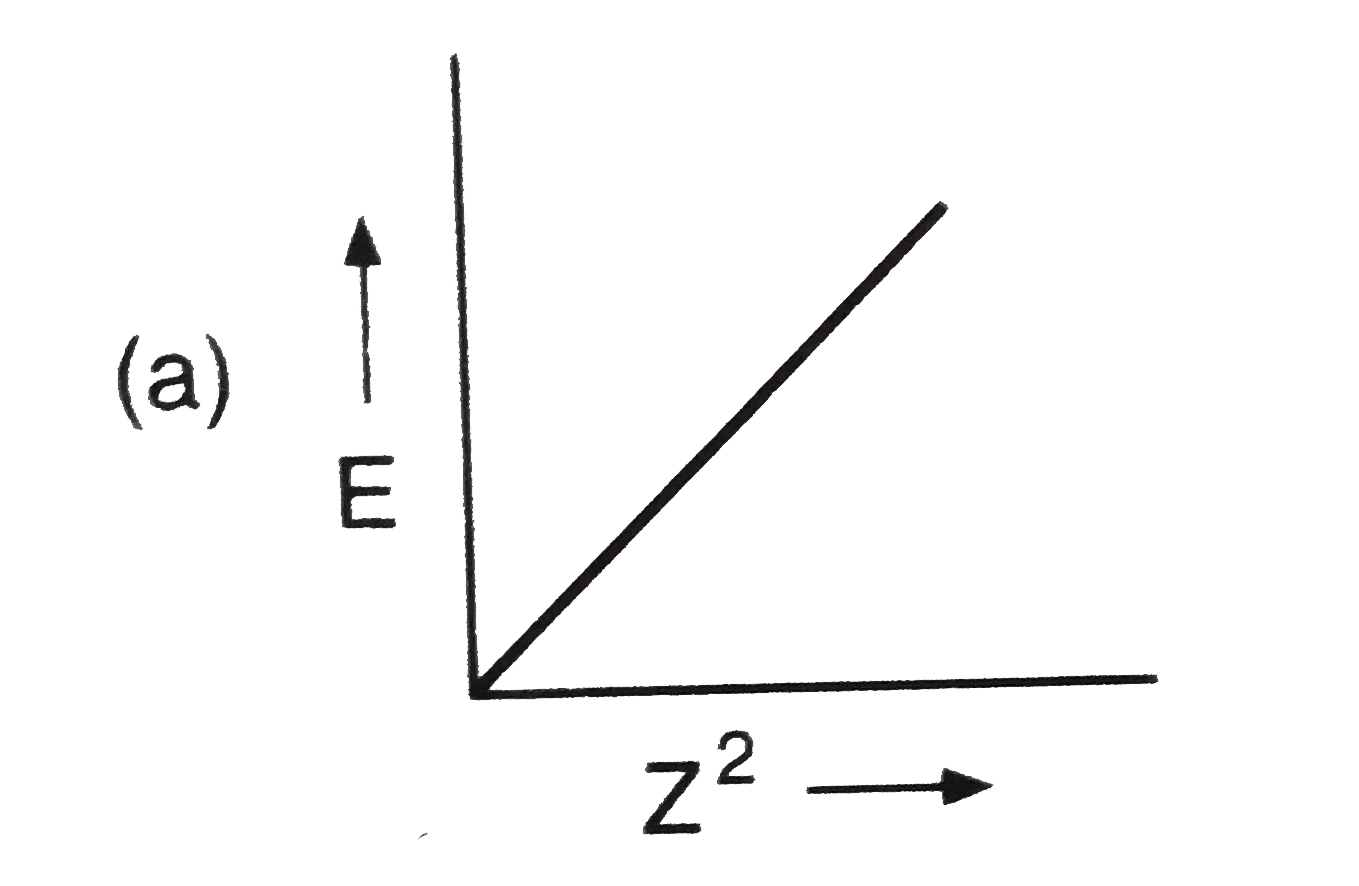

The correct Answer is:D
To solve the question regarding the variation of electron energy with atomic number, we can follow these steps:
Step 1: Understand the Energy Formula
The energy of an electron in an atom can be expressed using the formula:
E=−13.6Z2n2
where:
- E is the energy of the electron,
- Z is the atomic number,
- n is the principal quantum number (energy level).
Step 2: Identify the Relationship
From the formula, we can see that the energy E is directly proportional to the square of the atomic number Z when n is constant. Thus, we can express this relationship as:
E∝Z2
Step 3: Graphical Representation
Since the energy is proportional to Z2, if we were to plot a graph of energy E against Z2, we would expect a linear relationship. The graph would pass through the origin (0,0) because when Z=0, E will also be 0.
Step 4: Conclusion
Based on the analysis, we can conclude that as the atomic number Z increases, the energy of the electron also increases proportionally to the square of the atomic number. Therefore, the correct option based on the relationship is that the energy of the electron varies with the atomic number in a way that can be represented by a straight line graph passing through the origin.
Final Answer
The energy of the electron varies with atomic number Z as E∝Z2, and the graph of energy versus Z2 will be a straight line passing through the origin.
---
The energy of an electron in an atom can be expressed using the formula:
E=−13.6Z2n2
where:
- E is the energy of the electron,
- Z is the atomic number,
- n is the principal quantum number (energy level).
From the formula, we can see that the energy E is directly proportional to the square of the atomic number Z when n is constant. Thus, we can express this relationship as:
E∝Z2
Since the energy is proportional to Z2, if we were to plot a graph of energy E against Z2, we would expect a linear relationship. The graph would pass through the origin (0,0) because when Z=0, E will also be 0.
Based on the analysis, we can conclude that as the atomic number Z increases, the energy of the electron also increases proportionally to the square of the atomic number. Therefore, the correct option based on the relationship is that the energy of the electron varies with the atomic number in a way that can be represented by a straight line graph passing through the origin.
The energy of the electron varies with atomic number Z as E∝Z2, and the graph of energy versus Z2 will be a straight line passing through the origin.
Topper's Solved these Questions
- MISCELLANEOUS (TOPICS OF GENERAL INTEREST)BOOK - OP TANDONCHAPTER - MISCELLANEOUS (TOPICS OF GENERAL INTEREST)EXERCISE - SET-V: Matching type Questions
37 Videos
- INTRODUCTION TO ORGANIC CHEMISTRY BOOK - OP TANDONCHAPTER - INTRODUCTION TO ORGANIC CHEMISTRY EXERCISE - SINGLE INTEGER ANSWER TYPE
4 Videos
- OXIDATION AND REDUCTION (REDOX REACTIONS)BOOK - OP TANDONCHAPTER - OXIDATION AND REDUCTION (REDOX REACTIONS)EXERCISE - SECTION V
3 Videos
Similar Questions
Knowledge Check
Energy of electron in the H-atom is determined by
Aonly nBboth n and lCn, l and mDall the four quantum numbers.Energy of electron in a orbit of H -atom is
APositiveBNegativeCZeroDNothing can be saidThe variation of wavelength λ of the Kα line with atomic number Z of the target is shown by the following curve of
 AABBCCDNone of these
AABBCCDNone of these
The quantum number of the last electron of an element are below pralict the atomic number and same of the electron from the following quantum number
View SolutionThe wavelength λ of the Ka line of characteristic X - ray spectra varies with atomic number approximately
View SolutionAn electron transits from n=3 to ground state in hydrogen atom. If K, P and T are kinetic energy, potential energy and total energy of the electron respectively, which of the following statements regarding the energy of electron is/are correct?
View SolutionEnergy of the electron in Hydrogen atom is given by
View SolutionThe total energy of the electron in atom is
View Solution
