Question

For a closed container containing 10 moles of an ideal gas, at constant pressure of $0.82$ atm, which graph correctly represent, variation of log V us log T where volume is in litre and temp. in kelvin :

Options

A.
B.
C.
D.

Answer

a

Explanation

To solve the problem of determining which graph correctly represents the variation of log V versus log T for a closed container containing 10 moles of an ideal gas at a constant pressure of 0.82 atm, we can follow these steps:

1. Understand the Ideal Gas Law:
The ideal gas law is given by the equation:
\( PV = nRT \)
where \( P \) is pressure, \( V \) is volume, \( n \) is the number of moles, \( R \) is the ideal gas constant, and \( T \) is temperature.

2. Rearrange the Ideal Gas Law:
We need to express volume \( V \) in terms of temperature \( T \). Rearranging the ideal gas law gives:
\( V = \frac{nRT}{P} \)

3. Take the Logarithm of Both Sides:
To find the relationship between log V and log T, we take the logarithm of both sides:
\( \log V = \log\left(\frac{nRT}{P}\right) \)
This can be expanded using properties of logarithms:
\( \log V = \log(nR) + \log T - \log P \)

4. Identify Constants:
Since \( n \) (10 moles), \( R \) (0.082 atm·L/(mol·K)), and \( P \) (0.82 atm) are constants, we can combine them:
\( \log V = \log T + \text{constant} \)
Here, the constant is \( \log(nR/P) \).

5. Determine the Slope and Intercept:
The equation can be rewritten in the form:
\( \log V = \log T + \text{constant} \)
This indicates that the slope (m) is 1, and the y-intercept (C) is the constant value \( \log(nR/P) \).

6. Calculate the Constant:
We can calculate the constant:
\( n = 10, \quad R = 0.082, \quad P = 0.82 \)
\( \log\left(\frac{nR}{P}\right) = \log\left(\frac{10 \times 0.082}{0.82}\right) = \log(1) = 0 \)
Thus, the y-intercept is 0.

7. Final Equation:
Therefore, we have:
\( \log V = \log T \)
This indicates a linear relationship with a slope of 1 and a y-intercept of 0.

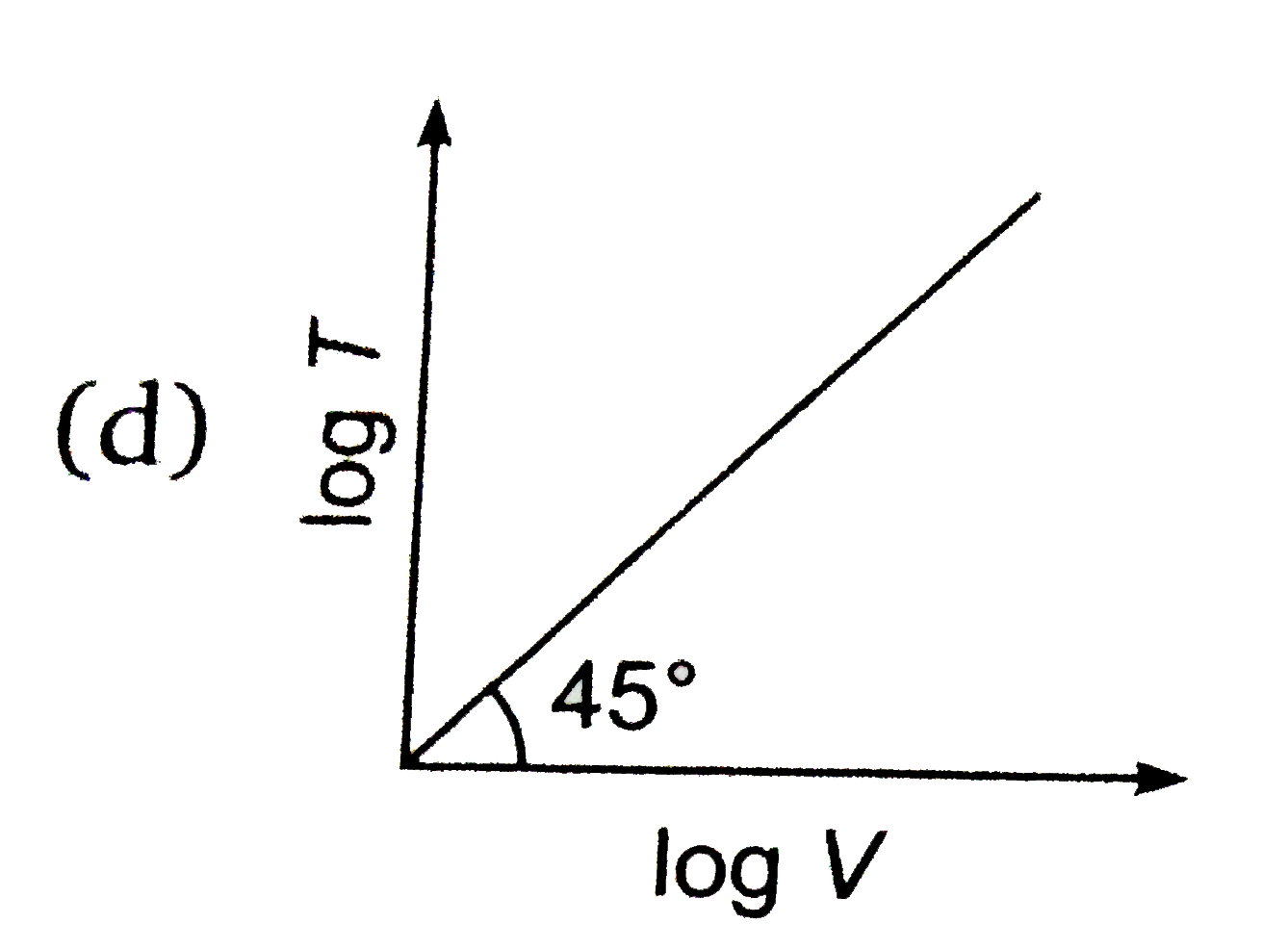
8. Graph Interpretation:
The graph of \( \log V \) versus \( \log T \) will be a straight line passing through the origin (0,0) with a slope of 1, which corresponds to an angle of 45 degrees.

Conclusion:
The correct graph that represents the variation of log V versus log T is the one that shows a straight line with a slope of 1 and passes through the origin.