For a reaction ,the value of slope of a plot in K→1T=……….
−Ea2.303
−EaR
−Ea
−Ea2.303R
The correct Answer is:B
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - KUMAR PRAKASHANCHAPTER - CHEMICAL KINETICSEXERCISE - Section-E(MCQs asked in JEE/NEET/AIEEE)
34 Videos
- BOARD EXAM QUESTION PAPER MARCH - 2020 BOOK - KUMAR PRAKASHANCHAPTER - BOARD EXAM QUESTION PAPER MARCH - 2020 EXERCISE - PART -B
23 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - KUMAR PRAKASHANCHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - SECTION - E (MCQs ASKED IN GUJCET/BOARD EXAM)
37 Videos
Similar Questions
Knowledge Check
In accordance to Arrhenius equation, the plot of log k against 1T is a straight line. The slope of the line is equal to
A−EaRB−2.303Ea.RC−Ea2.303RD−Ea2.303For a first order reaction, the plot of log k against 1/T is a straight line. The slope of the line is equal to
AEaRB2.303Ea×RCEa2.303D−Ea2.303RIf a graph is plotted between ln k and 1/T for the first order reaction, the slope of the straight line so obtained is given by
A−EaRB−Ea2.303RC−2.303EaRD−Ea2.303
The slope of Arrhenius Plot (lnK v/s 1/T) of 1st order reaction is -5x103K. The value of Ea of the reaction is.
View SolutionRate constant k of a reaction varies with temperature according to the equation
logk = constant −Ea2.303R(1T)
where Ea is the energy of activation for the reaction . When a graph is plotted for log k versus 1T , a straight line with a slope - 6670 K is obtained. Calculate the energy of activation for this reaction
View SolutionRate constant k of a reaction varies with temperature according to the equation
logk = constant −Ea2.303R(1T)
where Ea is the energy of activation for the reaction . When a graph is plotted for log k versus 1T , a straight line with a slope - 6670 K is obtained. Calculate the energy of activation for this reaction
View SolutionWhen a plot between logk and 1/T is plotted we get the graph as shown.
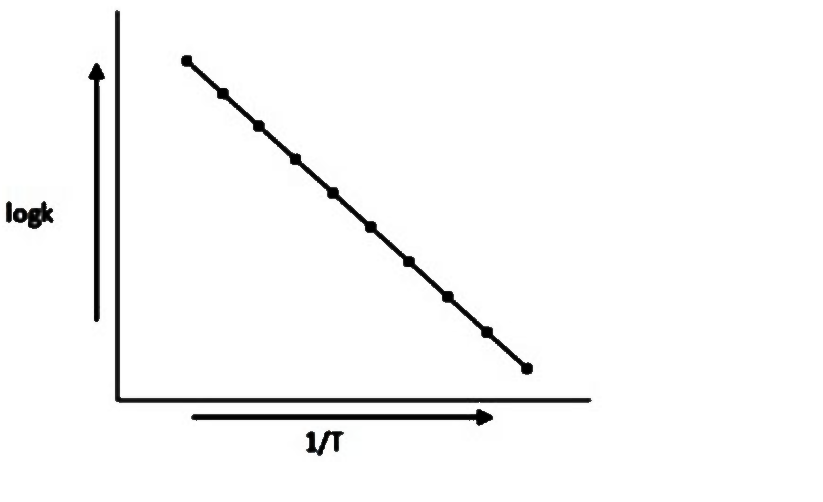
What is the value of slope in the graph?
View SolutionFor a first order reaction, the reaction, the plot of logC against 't' (log C vs 't') gives a straight line with slope equal to:
View Solution
