For the first order thermal decomposition reaction, the following data were obtained :
Calculate the rate constant
(Given : log 2= 0.301, log 3 = 0.4771, log 4=0.6021)
To calculate the rate constant (k) for the first-order thermal decomposition reaction of ethyl chloride, we can use the following formula:
k=2.303tlog(P0P0−Pt)
Where:
- k = rate constant
- t = time (in seconds)
- P0 = initial pressure (at t=0)
- Pt = pressure at time t
1. Identify the Initial and Final Pressures:
- From the data provided:
- At t=0 seconds, P0=0.30 atm
- At t=300 seconds, Pt=0.50 atm
2. Calculate the Change in Pressure:
- The change in pressure is given by:
P0−Pt=0.30atm−0.50atm=−0.20atm
However, since we are looking for the pressure of the products formed, we should consider the pressure increase:
Pt−P0=0.50atm−0.30atm=0.20atm
3. Plug Values into the Rate Constant Formula:
- Substitute t=300 seconds, P0=0.30 atm, and Pt−P0=0.20 atm into the formula:
k=2.303300log(0.300.20)
4. Calculate the Logarithm:
- Calculate 0.300.20=1.5
- Now, we need to calculate log(1.5):
- Using the change of base formula, we can express log(1.5) as:
log(1.5)=log(3)−log(2)(using known values)
- Given log(3)=0.4771 and log(2)=0.301:
log(1.5)=0.4771−0.301=0.1761
5. Substitute the Logarithm Back into the Equation:
- Now substitute log(1.5) back into the rate constant equation:
k=2.303300×0.1761
6. Calculate the Rate Constant:
- Performing the multiplication:
k=2.303×0.1761300=0.4057300≈0.0013523atm−1s−1
7. Final Result:
- The rate constant k is approximately:
k≈0.00135s−1
- k = rate constant
- t = time (in seconds)
- P0 = initial pressure (at t=0)
- Pt = pressure at time t
- From the data provided:
- At t=0 seconds, P0=0.30 atm
- At t=300 seconds, Pt=0.50 atm
- The change in pressure is given by:
P0−Pt=0.30atm−0.50atm=−0.20atm
However, since we are looking for the pressure of the products formed, we should consider the pressure increase:
Pt−P0=0.50atm−0.30atm=0.20atm
- Substitute t=300 seconds, P0=0.30 atm, and Pt−P0=0.20 atm into the formula:
k=2.303300log(0.300.20)
- Calculate 0.300.20=1.5
- Now, we need to calculate log(1.5):
- Using the change of base formula, we can express log(1.5) as:
log(1.5)=log(3)−log(2)(using known values)
- Given log(3)=0.4771 and log(2)=0.301:
log(1.5)=0.4771−0.301=0.1761
- Now substitute log(1.5) back into the rate constant equation:
k=2.303300×0.1761
- Performing the multiplication:
k=2.303×0.1761300=0.4057300≈0.0013523atm−1s−1
- The rate constant k is approximately:
k≈0.00135s−1
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - C.B.S.E CLASS XII
41 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - DELHI BOARD SET II
9 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-III
34 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION: D
1 Videos
Similar Questions
For the first order thermal decomposition reaction, the following data were obtained:
C2H5Cl(g)→C2H4(g)+HCl(g)
Time/secondTotal pressure/atm 0 0.30 300 0.50
Calculate the rate constant. [Given : log 2 = 0.301, log 3 = 0.4771, log 4 = 0.6021]
View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume :
SO2Cl2(g)→SO2(g)+Cl2(g)
Experiment Times/s−1 Total pressure/atm1 0 0.42 100 0.7
Calculate the rate constant. Given : log 4 = 0.6021, log 2 = 0.3010)
View Solution
Knowledge Check
In the reaction, CH3COCH3(g)→C2H4(g)+H2(g)+CO(g) the initial pressure is found to be 0.40 atm and after 10 min, it was 0.50 atm. The rate constant for first order reaction is [log 4 = 0.6021, log 3.5 = 0.5441]
A0.0133 −1minB0.4 s−1C10 s−1D0.6 −1min
The following data were obtained during the first order thermal decomposition of SO2Cl2 at constant volume :
ExperimentTime (s)Total Pressure (atm)100.321000.5
Calculate rate constant
[Given : log 6 = 0.7782, log 3 = 0.4771]
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5 (g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
(S.no,Time,Total Pressure / atm),(1,0,0,5),(2,100,0.512)
Calculate the rate constant.
View SolutionThe following data were obtained the first order thermal decomposition of N2O5(g) at constant volume : 2N2O5(g)→2N2O4(g)+O2(g)
S. No.Time/sTotal pressure (atm)100.521000.512
Calculate the rate constant.
View SolutionThe following data were obtained during the first thermal decompoistion of N2O5(g) at constant volume.
2N2O5(g)→2N2O4(g)+O2(g)
∣∣ ∣ ∣∣S.No.Time (s)Total pressure (atm)i.00.5ii.1000.512∣∣ ∣ ∣∣
Calculate the rate constant.
View SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)
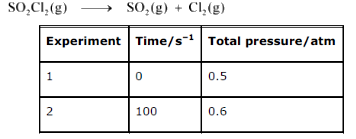
Calculate the rate of the reaction when total pressure is 0.65 atm
View SolutionThe following rate data were obtained for the thermal decomposition of N2O5(g)
2N2O5(g)→2N2O4(g)+O2(g)
Time (sec)050Total pressure (atm)0.20.25
Calculate the reaction rate when the total pressure is 0.28 atm
View SolutionA first order reaction takes 10 minutes for 25% decomposition. Calculate t1/2 for the reaction.
[Given : log 2 = 0.3010, log 3 = 0.4771, log 4 = 0.6021]
View Solution
