Given that the temperature coefficient for the saponification of ethylacetate by NaOH is 1.75. Calculate the activation energy.
10.7kcal mol−1
12.7kcal mol−1
14.7kcal mol−1
16.7kcal mol−1
The correct Answer is:A
m=KT+10K=1.75
logKT+10K=Ea2.303[125−135]
log1.75=Ea2.303×2[10875]
Ea=10.7 kcal mol−1
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - A2ZCHAPTER - CHEMICAL KINETICSEXERCISE - Parallel Reaction, Consecutive Reaction, Special Cases Of First-Order Reactions
25 Videos
- CHEMICAL KINETICSBOOK - A2ZCHAPTER - CHEMICAL KINETICSEXERCISE - Section B - Assertion Reasoning
21 Videos
- CHEMICAL KINETICSBOOK - A2ZCHAPTER - CHEMICAL KINETICSEXERCISE - Initial Rate Method And Ostwaid Method
18 Videos
- BIOMOLECULESBOOK - A2ZCHAPTER - BIOMOLECULESEXERCISE - Section D - Chapter End Test
30 Videos
- COORDINATION COMPOUNDSBOOK - A2ZCHAPTER - COORDINATION COMPOUNDSEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
If the temperature coefficient for hydrolysis of ester by NaOH is 2, then the activation energy for ten degree rise of temperature from 298 K is:
A42.74kJ/molB52.89kJ/molC5.28kJ/molD4.27kJ/molArrhenius studied the effect of temperature on the rate of a reaction and postulated that rate constant varies with temperature exponentially as k=Ae−Ea/RT. For most of the reactions, it was found that the temperature coefficient of the reaction lies between 2 to 3. The method is generally used for finding the activation energy of a reaction. Keeping temperature constant, the effect of catalyst on the activation energy has also been studied by studying how much the rate of reaction changes in the presence of catalyst. In most of the cases, it is observed that catalyst lowers the activation energy barrier and increases the rate of reaction.
If the rate of reaction grows 15.6 times on increasing the temperature by 30 K, the temperature coefficient of the reaction will be nearlyA2B2.5C3.0D3.5Arrhenius studied the effect of temperature on the rate of a reaction and postulated that rate constant varies with temperature exponentially as k=Ae−Ea/RT. For most of the reactions, it was found that the temperature coefficient of the reaction lies between 2 to 3. The method is generally used for finding the activation energy of a reaction. Keeping temperature constant, the effect of catalyst on the activation energy has also been studied by studying how much the rate of reaction changes in the presence of catalyst. In most of the cases, it is observed that catalyst lowers the activation energy barrier and increases the rate of reaction.
If the rate of reaction doubles for 10∘ rise of temperature from 290 K to 300 K, the activation energy of the reaction will be approximatelyA40 kJ mol−1B50 kJ mol−1C60 kJ mol−1D70 kJ mol−1
Given the following data, calculate coefficient of variation:
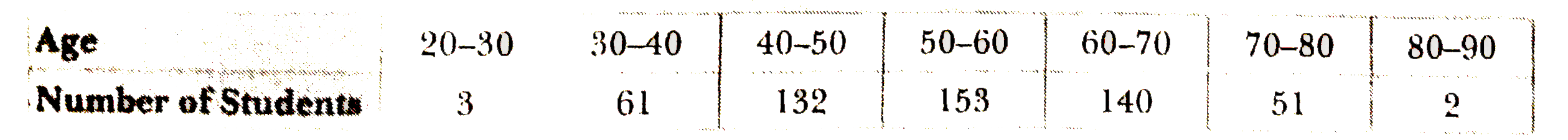
View SolutionThe rates of most reactions double when their temperature is raised from 298 K to 308 K. Calculate their activation energy.
View SolutionThe temperature coefficient of a reaction is 2 and the rate of reaction at 25° C is 3molL−1−1min . Calculate the rate at 75∘C
View SolutionThe viscosity of mercury decreases with the rise in temperature (Table 21.1a). Check whether relation (34.10) is valid for mercury. Calculate the activation energy.

View SolutionArrhenius studied the effect of temperature on the rate of a reaction and postulated that rate constant varies with temperature exponentially as k=Ae−Ea/RT. For most of the reactions, it was found that the temperature coefficient of the reaction lies between 2 to 3. The method is generally used for finding the activation energy of a reaction. Keeping temperature constant, the effect of catalyst on the activation energy has also been studied by studying how much the rate of reaction changes in the presence of catalyst. In most of the cases, it is observed that catalyst lowers the activation energy barrier and increases the rate of reaction.
If x is the fraction of molecules having energy greater than Ea, it will be given by
View Solution
