Hydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
Here,
is the Rydberg Constant, is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion. the wavelength of first line of balmer region.
The correct Answer is:
To solve the problem regarding the wavelength of the first line of the Balmer region for the hydrogen atom, we can follow these steps:
Step 1: Understand the Formula
The formula provided is:
1λ=RH(122−1n2)
where RH is the Rydberg constant, λ is the wavelength, and n is the principal quantum number of the electron's orbit.
Step 2: Identify the Values
For the first line of the Balmer series, we need to set n=3 (since the first line corresponds to the transition from n=3 to n=2). We also have:
RH=109678cm−1
Step 3: Substitute the Values into the Formula
Substituting n=3 into the formula gives:
1λ=RH(122−132)
Calculating the individual terms:
122=14and132=19
Thus,
1λ=109678(14−19)
Step 4: Calculate the Difference
Now, we need to calculate 14−19:
14−19=936−436=536
Step 5: Substitute Back into the Formula
Now substituting this back into our equation:
1λ=109678×536
Step 6: Calculate 1λ
Calculating 109678×536:
1λ=54839036≈15232.5cm−1
Step 7: Find λ
To find λ, take the reciprocal:
λ=115232.5≈0.0000655cm
Converting this to angstroms (1 cm = 108 angstroms):
λ≈6569Å
Final Answer
The wavelength of the first line of the Balmer region is approximately:
λ≈6569Å
The formula provided is:
1λ=RH(122−1n2)
where RH is the Rydberg constant, λ is the wavelength, and n is the principal quantum number of the electron's orbit.
For the first line of the Balmer series, we need to set n=3 (since the first line corresponds to the transition from n=3 to n=2). We also have:
RH=109678cm−1
Substituting n=3 into the formula gives:
1λ=RH(122−132)
Calculating the individual terms:
122=14and132=19
Thus,
1λ=109678(14−19)
Now, we need to calculate 14−19:
14−19=936−436=536
Now substituting this back into our equation:
1λ=109678×536
Calculating 109678×536:
1λ=54839036≈15232.5cm−1
To find λ, take the reciprocal:
λ=115232.5≈0.0000655cm
Converting this to angstroms (1 cm = 108 angstroms):
λ≈6569Å
The wavelength of the first line of the Balmer region is approximately:
λ≈6569Å
Similar Questions
Hydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
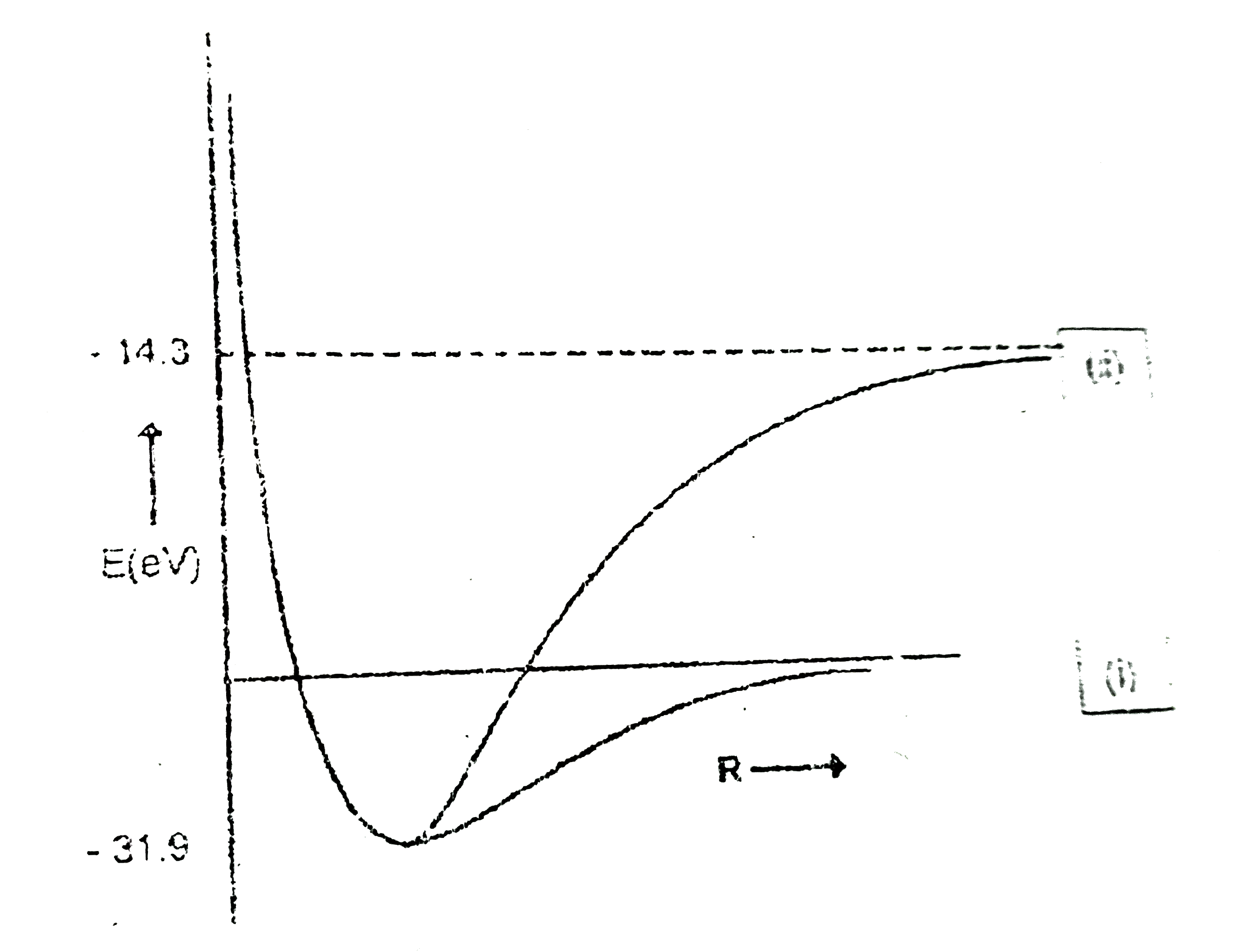
Put appropriate channel labels (i) or (ii) in the boxes below
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Determine the values of the dissociation energies (DeineV) of the H2 molecule corresponding to channel (i)
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
From the given data, calculate the energy change for the process
H−→H+e−
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
H− is a two-electron atomic system. Assuming that the Bohr energy formula is valid for each electron with nuclear charge Z replaced by Zeff' calculate Zeff for H−.
View SolutionThe observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher. Balmer's empirical formula is (1)/(lambda) = R_(H)[(1)/(2^(2)) - (1)/(n^(2))] = n = 3, 4,5… R_(H) = 109678 cm^(-1) is the Rydberg constant. Niels Bohr derived this expression theoretically in 1913. The formula is a generalised to any on electron atom/ion. How many lines in the spectrum will be observed when electrons returns from 7th shell to 2nd shell ?
View SolutionThe observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher. Balmer's empirical formula is (1)/(lambda) = R_(H)[(1)/(2^(2)) - (1)/(n^(2))] = n = 3, 4,5… R_(H) = 109678 cm^(-1) is the Rydberg constant. Niels Bohr derived this expression theoretically in 1913. The formula is a generalised to any on electron atom/ion. The wavelength of first line of Balmer spectrum of hydrogen will be :
View SolutionThe observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher. Balmer's empirical formula is
1λ=RH[122−1n2]=n=3,4,5…
RH=109678cm−1 is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is a generalised to any on electron atom/ion.
Which of the following is not correctly matched ?
View SolutionThe observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher. Balmer's empirical formula is
1λ=RH[122−1n2]=n=3,4,5…
RH=109678cm−1 is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is a generalised to any on electron atom/ion.
The wavelength of first line of Balmer spectrum of hydrogen will be :
View Solution
